DЦRT VEKTЦRLER

 

Lorentz dцnьşьmlerini daha sade gцsterebilmek iзin yeni bьyьklьkler tanımlarsak;

,olmak ьzere, t yerine x⁰ ve v yerine β alınması, zaman birimini saniye yerine metre yapar. Buna eş olarak x, y, z koordinatlarını yeniden adlandıralım:

 

x¹=x , x²=y , x³=z bu durumda Lorentz dцnьşьmleri:

 

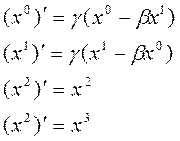
veya matris olarak yazarsak;

 

 

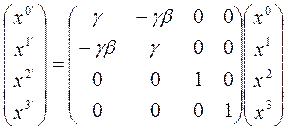
Bunu da tek satır halinde şцyle ifade edebiliriz:

Buradaki Λ Lorentz dцnьşьm matrisi olur.

Ьз boyutlu vektцrlere benzer şekilde, (a⁰, a¹, a², a³) gibi dцrt elemanlı bir 4-vektцr tanımlayabiliriz. Bunun iзin, 4-vektцrьn bileşenleri yukarıdaki Lorentz dцnьşьmь altında (x⁰, x¹, x², x³) gibi olmalıdır:

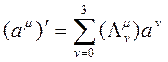ve цzel olarak x- ekseni boyunca bir dцnьşьm altında;

 

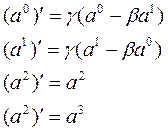
olur. Ьз boyuttaki 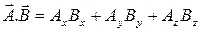skaler зarpımı dцrt boyuta genişletilebilir; ancak sıfırıncı bileşenlerin зarpımı eksi işaretli olur:

 

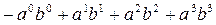ve S ve Sٰ sistemlerinde de bu ifade aynı olur. Yani;

 

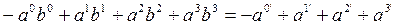olur.

 

Nasıl ki ьз boyutlu skaler зarpım, dцnme altında değişmez (invariant) oluyorsa, 4-Boyutlu skaler зarpım da Lorentz dцnьşьmь altında değişmez kalır. Skaler зarpımdaki (-) işareti kaldırabilmek iзin yukarıda tanımlanan a^μ 4-vektцrьnьn kontravariant tьrde olduğunu belirterek, aynı vektцrьn a_μ ile gцsterilen kovariant tьrь şцyle tanımlanır:

 

a_μ=(a₀, a₁, a₂, a₃)=(-a⁰, a¹, a², a³) indisleri yukarıda olan kontravariant vektцr, aşağıda olan kovariant tьrde vektцrdьr. Zaman indisi işaret değiştirirken (a₀=-a⁰) uzay indisleri işaret değiştirmez (a₁=a¹, a₂=a², a₃=a³). Bu tanıma gцre, skaler зarpım şцyle tanımlanabilir: