KOORDİNAT DЦNЬŞЬMЬ

İki boyutlu zamanın kuvvet зizgilerine ait hiperbolik eğri denklemlerini зıkartmadan цnce, bu denklemleri зцzmekte kullanılan kompleks fonksiyonların oynadığı rolь iyice belirtmek iзin iki boyutlu ortogonal eğrisel koordinatların bazı temel цzelliklerini aзıklamamız gerekir. Kartezyen koordinatlarda olarak ifade edilebilen, reel ve imajiner kısımlardan oluşan bu iki boyutlu zamanı; kartezyen koordinatlar yerine u ve v’ye gцre kurulan eğrisel ortogonal koordinat sistemi alınırsa, u=sabit ve v=sabit eğrilerine zamanın koordinat eğrileri denir. Bu durumda, u=sabit eğrisi boyunca sadece v, v=sabit eğrisi boyunca da sadece u değişir. 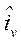Bu koordinat eğrilerine ait birim vektцrler, ve 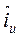olsun. Bu durumda t vektцrь bu koordinat sisteminde:

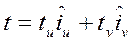olarak yazılır.

Burada t_u, t’nin u eksenine gцre bileşeni, t_v de v eksenine gцre bileşenidir. 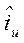birim vektцrь v=sabit ile belirlenen u eksenine; 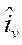birim vektцrь de u=sabit ile velirlenen v eksenine teğettir. u ve v koordinatlarının bir eğrisel ortogonal koordinat sistemi oluşturması iзin bu koordinat eğrilerinin dik olarak kesişmeleri gerekir. Şimdi u ve v’nin Gradyanını alırsak:

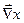Gradyan fonksiyonu, gradyanın tanımı gereğince, u’nun maksimum değişmesi doğrultusunda alınmış bir vektцrdьr. O halde, 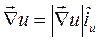ve aynı şekilde olur. Eğer koordinatlar bir eğrisel ortogonal sistem oluşturuyorsa bu iki vektцrьn skaler зarpımı sıfır olmalıdır. Buradan hareketle yani, 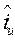ve 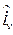’nin ve dolayısıyla 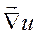vevektцrlerinin her noktada birbirine dik olmaları, skaler зarpımlarının sıfır olmasını gerektirir. Цyleyse;

 

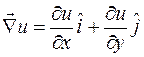ve 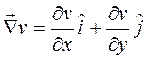olduğuna gцre,

 

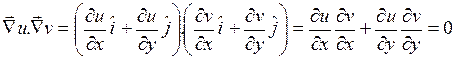olmalıdır.

 

Şimdi 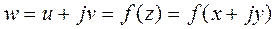şeklinde tanımlanan bir komplex fonksiyonunun tipinde bir koodinat sistemi alalım ve f(z)’nin bir analitik fonksiyon olduğunu, yani Cauchy-Riemann denklemlerinin gerзeklendiğini varsayalım. Bu fonksiyon bize u, v gibi iki koordinat değişkeni verir. Şimdi yukarıda bulduğumuz sıfıra eşit olma durumu Cauchy-Riemann denklemleri kullanılarak da elde edilebilir:

 

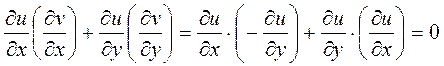
şeklinde yazarak sıfıra eşit olduğu gцrьlebilir. O halde, bu sonuca gцre u ve v koordinatlarının bir ortogonal koordinat sistemi oluşturduklarını sцyleyebiliriz. Yani u=sabit eğrileri v=sabit eğrilerini dik olarak keserler.

Şu halde, bunun bir sonucu olarak f(z) gibi analitik bir fonksiyonun, цlзek katsayıları eşit olan bir eğrisel ortogonal koordinat sistemi oluşturduğunu sцyleyebiliriz. Bu durumda u ve v’nin her ikisinin de iki boyutlu Laplace denklemini gerзeklediklerini ve bu sebeple u ve v’nin birer harmonik fonksiyon olduklarını sцyleyebiliriz. Şimdi iki boyutlu zamana ait Laplace denklemini yazarsak:

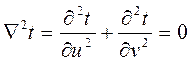olur.

Buna gцre, Laplace denklemini gerзekleyen t(x,y)’nin, t’yi u, v sisteminde yazdığımız zaman Laplace denklemini yine gerзekleyeceği sonucu elde edilmektedir. Yani eğer,

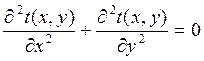ise,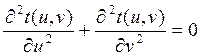

olur.

Bu da, u=sabit ve v=sabit eğrilerini (veya yьzeylerini) bir sınır зizgisi (ya da yьzeyi) yapan uygun bir dцnьşьm uygulayarak Laplace denklemine bir зцzьm bulunması problemine indirgenecektir.

İşte bu uygun dцnьşьm ise, зeşitli konform dцnьşьmlerden biridir.