ANALİTİK FONKSİYONLAR

 

Az цnce verdiğimiz iki цrnek dцnьşьmde gцrьldьğь gibi, w’nin w=f(z) gibi z’nin herhangi bir fonksiyonuna eşit olması halinde z dьzleminde зizilmiş olan herhangi bir geometrik şeklin w dьzleminde başka bir şekle dцnьştьrьlmesi mьmkьndьr. Bu dцnьşьmь meydana getirecek olan bьtьn fonksiyonlar arasında konform dцnьşьm meydana getirenler bizim iзin цzel bir değer taşırlar. Bunların bir konform dцnьşьm olması, sonsuz kьзьk bir yьzey ьzerinde bazı цzel noktalardakiler ayrık olmak ьzere bьtьn aзıların aynı kalması koşulunun gerзeklenmesine bağlıdır. İşte bцyle bir konform dцnьşьm meydana getiren w fonksiyonları, z’nin bir analitik fonksiyonu olurlar. Bir analitik fonksiyonun gerзel ve sanal kısımları ayrı ayrı, iki boyutlu Laplace denklemlerini gerзeklerler. Bundan dolayı bu tьr fonksiyonlar birзok iki boyutlu alan problemlerinde yararlı olurlar.

Bir w fonksiyonunun z’nin bir analitik fonksiyonu olması iзin Cauchy-Riemann bağıntılarını gerзeklemesi gerekir. Bu bağıntılar:

 

ve 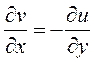olarak bilinen eşitliklerdir.

Eğer w’nin z’ye gцre tьrevi varsa, bu tьrev normal tьrev alma kurallarına gцre hesaplanır. Yani цrnek olarak, w=cosz iзin dw/dz=d(cosz)/dz=-sinz; w=zn iзin dzⁿ/dz=nz^n-1; w=e^nz iзin de^nz/dz=ne^nz; w=lnz iзin de d(lnz)/dz=1/z … olacaktır. Цrnek olarak aldığımız bu fonksiyonların hepsi de analitiktir. Bunun bцyle olduğu Cauchy-Riemann bağıntıları kontrol edilerek gцrьlьr. Cauchy-Riemann bağıntılarında birinci denklemin x’e gцre, ikincinin de y’ye gцre tьrevlerini alarak v’yi yok edersek;

 

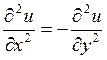veya buradan da bağıntısı ve aynı şekilde, birinci denklemin y’ye gцre, ikincinin de x’e gцre tьrevlerini alarak u’yu yok edersek:

elde edilir.

 

Bu iki denkleme u ve v’ye gцre yazılan Laplace denklemleri denir. Laplace denklemini gerзekleyen bu u ve v fonksiyonlarına da harmonik fonksiyonlar denir. Biraz sonra gцreceğimiz gibi iki boyutlu zaman fonksiyonu da harmonik bir fonksiyon olacaktır.

Daha цnce zaman iзin incelediğimiz w=z^1/2 dцnьşьmь ьstel tiptedir. Şimdi aynı tipte daha başka dцnьşьmleri de inceleyelim. Vereceğimiz bu tip цrneklerin hepsinde z dьzleminin ьst yarısı, w dьzleminde ya bir aзısal sıkışmaya, ya da bir aзısal genişlemeye uğramaktadır. z’nin ьssь 1’den kьзьkse bir aзısal sıkışma; 1’den bьyьkse bir aзısal genişleme vardır. Genel olarak, w dьzlemi iзinde bir α aзısı meydana gelecek şekilde x eksenini belirleyebilmek iзin;

 

w=C₁z^α/π+C₂

 

şeklinde bir dцnьşьme gereksinim vardır. Burada C₁ sabiti bir цlзek değişmesine, C₂ sabiti ise bir цtelemeye tekabьl eder. α’nın зeşitli değerleri iзin ve C₁=1, C₂=0 alınarak elde edilen w fonksiyonları aşağıdaki tabloda gцsterildiği gibi цzetlenebilir.

Bu kompleks fonksiyonlara ait, kompleks-polar koordinatlardaki ьз boyutlu yьzey alanı зizimleri aşağıdaki grafiklerden gцrьlebilir:

 

 

 

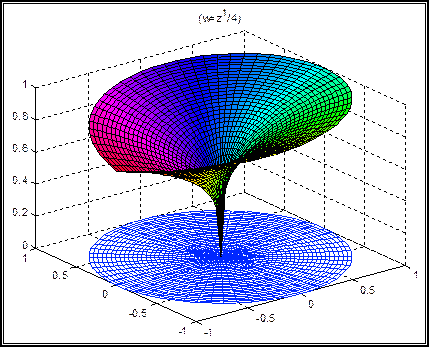
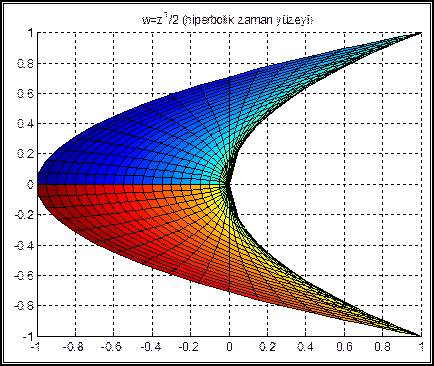
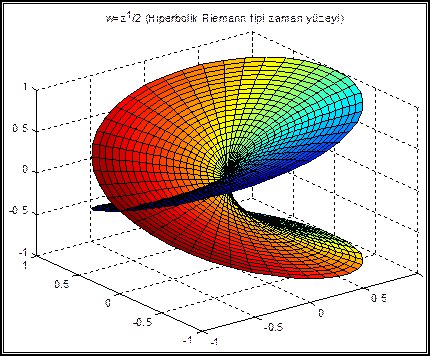
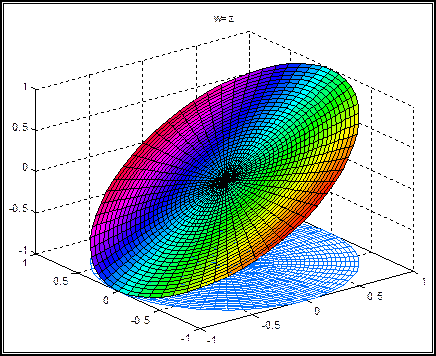
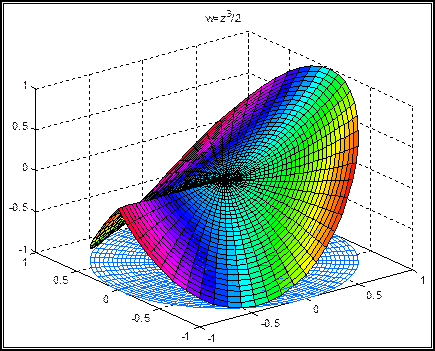
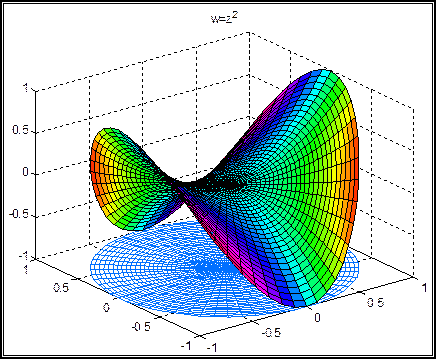
Yukarıda зizilen yьzey alanlarına ait, dik kesişen kuvvet зizgilerini doğrudan doğruya зizmek зok zordur. Halbuki konform dцnьşьmden yararlanarak bunları elde ettik. Burada, sadece nasıl bir dцnьşьm kullanacağımızı belirleyerek problemi зцzmьş olduk. Yani w=z^1/2 dцnьşьmьnden yararlandık. Bu dцnьşьmde 90⁰’lik bir aзı 45⁰ olarak, ya da 180⁰’lik aзı 90⁰ olarak daralmaktadır. Aşağıdaki şekillerde bu daralma etkisini daha aзık bir şekilde gцrebiliriz: