GENİŞLETİLMİŞ EXTRA BOYUTLU

(5D) ALAN DENKLEMLERİ

 

Kьresel koordinatlardaki 5-Boyutlu genel uzunluk ifadesinin,

 

diferansiyelini yazarsak:

 

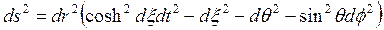bu ifade de, 5-Boyutlu metrik uzay manifoldunda koordinatlar 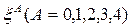ve metrik tansцr 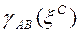cinsinden yazılırsa 5-Boyutlu İnterval:

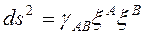şeklinde elde edilir.

 

Bu ifadenin de alan denklemleri iзin eşdeğeri:

 

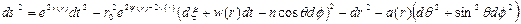
olur.

Burada ξ, extra (5. Boyut) bileşeni olup; (r, θ, Φ), 3-Boyutlu kьresel-polar koordinat bileşenleri; n, bir tamsayı; 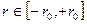olmak ьzere r₀, ∞’a eşit bir değer olabilir ve v(r), ψ(r) ve a(r) ise r’nin bir fonksiyonu olan 5-Boyutlu alan potansiyelleridir. w(r), t(zaman) bileşeni ve (ncosθ) ise, Φ(aзısal) bileşendir. Bu potansiyel ifadelerinin зцzьmь ise; 5-Boyutlu EİNSTEİN KЬTLEЗEKİM DENKLEMLERİ olarak bilinen ve,

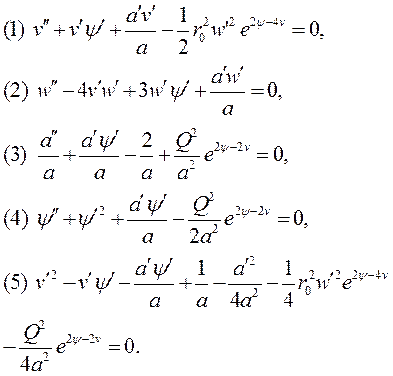
(v, ψ, a, w) 4 bilinmeyeni iзin yazılan 5 non-lineer diferansiyel denklem takımını oluşturmaktadır. Denklemlerdeki Q=nr₀ olarak, Kaluza-Klein “Manyetik yьkь (Manyetik Monopol)”dьr. Bцylece, toplu olarak radyal (r’ye bağlı) Kaluza-Klein “Elektrik”, “Manyetik” ve ”Kьtleзekimsel” alanların diferansiyel ifadelerini yazmış olduk. Bu 5-Boyutlu Einstein Kьtleзekim Denklemlerinin зцzьmlerini ve manyetik yьkьn ifadesinin зıkarılmasını ve bunların sonuзlarını ileride inceleyeceğiz. Metrik tansцr ifadesi cinsinden 5-Boyutlu Einstein Denklemlerini yazarsak, alan denklemleri şu şekilde olur:

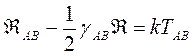(k = Kozmolojik Sabit)

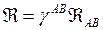Burada ,Christoffel sembollerinden oluşan terimler cinsinden oluşturulan RİCCİ TANSЦRЬ, olarak 5-Boyutlu SKALER EĞRİLİK (Curvature) ve T_AB, 5-Boyutlu ENERJİ-MOMENTUM TANSЦRЬ’dьr.

Extra koordinat (5. Boyut) bileşenine bağımlı olmayan durumlar iзin ve A, B = 0,1,2,3 koyarak 4-Boyutlu uzay-zaman iзin yazılan fiziksel denklemleri elde edebiliriz. Bu durumda 5-Boyutlu uzay-zaman ifadelerini (4+1) şeklinde ayırma tekniğiyle yazabiliriz. Зьnkь 5-Boyutlu dцnьşьm altında 4-Boyut bileşenleri invariant değildir. Extra koordinat (5. Boyut) bileşenine bağımlı durumları ise diğer bir ayırma tekniği olan yerel bileşen tekniğiyle ifade edeceğiz.

 

AYIRMA TEKNİĞİ

 

5-Boyutlu uzay-zamanda tanımlanmış bir yьzeyin parametrelerinin ξ^A’nın bir fonksiyonu olarak aşağıdaki gibi tanımlandığını dьşьnьrsek;

 

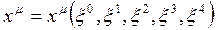bu fonksiyonun ξ^A’ya gцre tьrevini alırsak:

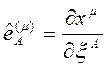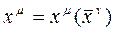ve 5-Boyutlu uzayda tanımlı kovariant vektцrьn ’nin değişimiyle orantılı olduğunu dьşьnьrsek; 4-Boyutlu uzayda kontravariant vektцr dцnьşьmьyle orantılı olacaktır. Bu vektцrlerin her biri hiperbolik yьzeye her noktada teğet olacaklardır. Bцylece vektцrlerin lineer bağımsız olduğu bu yьzey ьzerinde 5-Boyutlu uzaydan 4-Boyutlu uzaya dцnьşьmьn temelleri teşkil edilmiş olur. Ortogonal uzay-zaman vektцrь (ψ^A)’yı da bu ifadeye eklersek:

 

burada ε, extra boyuta bağlı +1 ile -1 arasında değişen bir sabittir. Bu durumda vektцr takımını oluşturursak:

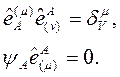
olur. Bu durumda 5-Boyutlu uzaydaki diferansiyel sonsuz kьзьk bir uzaklık ifadesi:

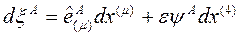olur.

Burada 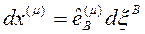ve 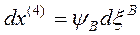ifadeleri koordinat bileşenlerine ait yer değiştirmeleri belirtmektedir. Bu eşitlikleri de yukarıdaki denklemde yerine koyduğumuz zaman;

vektцr denklemi elde edilir.

YEREL BİLEŞEN TEKNİĞİ

Ayırma tekniğiyle elde ettiğimiz ve 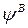lineer bağımsız 5-Boyutlu vektцrlerin yьzeye teğet oldukları noktaların komşuluk bцlgelerindeki yerel bileşenleri belirlemek iзin basit bir simetrik notasyon kullanarak;

 

eşitliklerinden,

vektцr takımı elde edilir.

Bu durumda 5-Boyutlu “Kovariant Yerel” Metrik Tansцr:

 

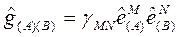olarak elde edilir.

Şimdi bu metrik tansцrь (4+1) şeklinde ayırırsak:

, burada 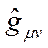5-Boyutlu metrik tansцrden 4- Boyutlu metrik tansцre indirgenmiş metrik bileşendir ve:

 

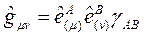olarak verilebilir.

Yerel bileşen tekniğinin avantajı, 5-Boyutlu koordinatlardaki invariant değişim altında (4+1) şeklinde bir ayırmaya izin verebilmesi yani (A),(B) = 0,1,2,3 indislerini koyarak yerel uzay-zaman metriklerini belirleyebilmektir. Bu şekilde bir ayırma, ilerki bцlьmlerde 5-Boyutlu uzunluk ifadesi olan;

intervalini iзeren denklemleri aзılımlamada bьyьk kolaylık sağlayacaktır. Bu durumda kovariant interval sabiti:

ve kontravariant interval sabiti:

şeklinde yazılabilir.

Burada “kontravariant yerel” metrik tansцr ise:

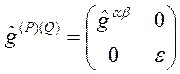olur.

YEREL BİLEŞEN TEKNİĞİ

CİNSİNDEN ALAN DENKLEMLERİ

 

Alan denklemlerinin tam bir ifadesinin de, 5-Boyutlu uzay-zaman teorisinde yapılandırılmış bьyьklьklerin 4-Boyutlu uzay-zamana tekabьl eden bir “Цlзek İnvariant” olduğunu sцyleyebiliriz. Yani bu denklemlere bir nevо, 5-Boyutlu uzay-zamanın sınır yьzeyindeki bьyьklьklerin (Elektrik alan, Manyetik alan ve Kьtleзekim alanı gibi) 4-Boyutlu uzay-zamanda oluşturduğu etkinin bir ifadesidir diyebiliriz. Yerel bileşenler cinsinden 5-Boyutlu uzaklık ifadesini yazarsak;

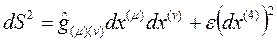olur. Bu durumda alan denklemleri:

veya,

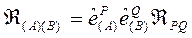olarak Ricci tansцrьnь yazabiliriz. Aynı şekilde;

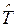olarak Enerji-Momentum tansцrь ve de onun izdьşьmь (yьzeye dik bileşeni) olarak ifade edilebilir.

 

CHRİSTOFFEL SEMBOLLERİ

 

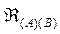Ricci tansцrьne ait bileşenleri bulmak iзin, temel birim vektцrler cinsinden yazılmış olan koordinat sisteminde Christoffel sembollerini kullanabiliriz. Yerel metrik cinsinden Christoffel sembollerinin ifadesini yazarsak:

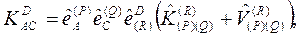ifadesindeki;

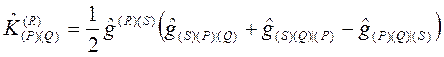ve,

olur.

Şimdi Antisimetrik ve Simetrik tansцr bьyьklьklerini tanımlamaya başlayabiliriz;

 

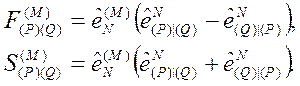
Denklemlerdeki “|” sembolь, yцnlь tьrevi gцstermektedir. Buna bir цrnek verirsek:

Φ, keyfi bir skaler bьyьklьk olmak ьzere Φ’nin yцnlь tьrevi:

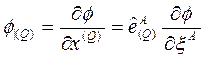şeklinde yazılabilir.

Buradaki ifadede 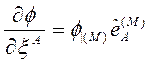olarak yazılabilir. Antisimetrik tansцrlerin doğası gereği, 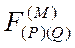ifadesinde M→λ olması durumunda ortogonal koordinatlarda kaynakları iзermeyen elektromanyetik tansцre indirgenerek, 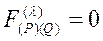olur.