BOYUTLU İNDİRGENMİŞ FİZİKSEL METRİK

 

4’ten fazla boyutları ifade etmek iзin, kullanacağımız geometrik bьyьklьklere ilişkin doğru teorik formьller oluşturmak gerekir. 5-Boyutlu uzayda ise, bu bьyьklьkler Antisimetrik Tansцr olan 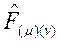, 4-vektцr olarak tanımlanan 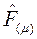ve Simetrik Tansцr 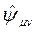’dir. Extra boyutları modellerken, Kaluza-Klein teorisinin kullandığı iki genelleştirme temel olarak, “Elektromanyetik Tansцr” diye adlandırılan bir tansцr ve “Skaler Alanların Gradyanı”dır. Diğer bir deyişle biri sьper-zar yapıdaki uzay zamanı (4-Boyutlu uzay-zamanın “sınır yьzeyindeki eğriliği”) temsil eden 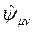Simetrik Tansцrь; ve diğeri de Elektromanyetik Tansцrь temsil eden 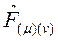Antisimetrik Tansцrьdьr. Bu iki fiziksel metrik bьyьklьk ise, 4-Boyutlu Enerji-Momentum Tansцrь olan 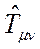ile ilişkili; 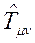tansцrь ise, Ricci Tans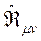цrь () ile bağlantılıdır.

 

5-Boyutlu fiziksel metrikten 4-Boyutluya indirgemede temel sorun, indirgenmiş metrik tansцrьn (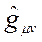) nasıl tanımlanacağıdır. Bunun iзin, en basit yanıt almak olur. Fakat bu tanımlama olası bьtьn fiziksel durumlar iзin geзerli değildir. Bunun iзin, metrik tansцrь belirli bir “Uydurma Faktцrь” ile зarpmamız gerekmektedir:

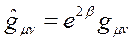olarak,

ifadedeki β, teorideki alanlar iзin kullanılan genişletme (Conform) faktцrьdьr. β, extra koordinata bağlı olarak değişen skaler bir sabittir. Bu varsayımımız uzay-zamandaki (4+1) şeklindeki ayırmayı etkilemeyecektir.

Bu durumda, matematiksel olarak indirgenmiş metriğe geзiş basitleşecektir. 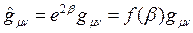ifadesini Christoffel sembolьnde yerine koyarsak,

Christoffel sembolь:

ve Ricci Tansцrь:

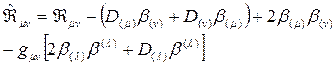
olarak yazılabilir. Burada, β_(α)=β_|(α) ve ile verilen diferansiyel kovariant operatцrь ile D arasındaki ilişki:

V, herhangi bir skaler alan olmak ьzere;

 

ve bцylece:

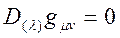olur.