GENEL DURUMDA 5-BOYUTLU İNDİRGENMİŞ ”KЬTLEЗEKİM ALAN TANSЦRЬNЬN” ELDE EDİLMESİ VE SONUЗLARI

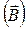Kьtleзekim Alanı , Manyetik Alan ve Elektrik Alanı 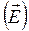iзin bulduğumuz bağıntılar, bunların ьз ayrı 4-vektцrьn uzay bileşenleri gibi davranmadıklarını gцsteriyor. Tersine, eylemsiz bir referans sisteminden diğerine geзtiğimizd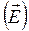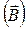e , ve’nin bileşenleri birbirine karışmaktadır. O halde dцnьşьm bağıntılarına uyan ve altı bileşenli olan bu bьyьklьk ne olabilir? Yanıt: İkinci dereceden 4-Boyutlu Antisimetrik bir Tansцr. Bцylece ilk ьз boyut uzayı, 4. Boyut ise “BEŞİNCİ BOYUT ZAMANINI” oluşturacaktır. İlk ьз boyut, sadece Elektrik Alan iзerirken; 4. Boyut Zamanı da iзerecektir; 5. Boyut ise Manyetizma ve Kьtleзekimini oluşturacaktır. 5. Boyut, ilk dцrt boyut ile bağlantısını bir KARADELİK TEKİLLİĞİ vasıtasıyla sağlayacaktır.

 

4-Vektцrlerin Lorentz dцnьşьmьnь hatırlarsak:

Burada Λ Lorentz dцnьşьm matrisidir. Eğer S’ sistemi x-yцnьnde v hızıyla gidiyorsa;

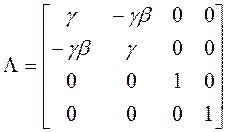olur.

ise, μ. satır v. sьtun elemanıdır. İkinci dereceden (yani iki indisli) bir tansцr dцnьşьrken, her bir indis iзin birer gerekir:

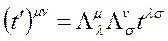
Dцrt boyutta ikinci dereceden tansцrьn 4Ч4=16 elemanı vardır;

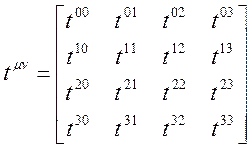
Fakat, 16 elemanın her biri farklı olmayabilir. Цrneğin, Simetrik Tansцr:

(Simetrik Tansцr)

olarak tanımlanır. Bu durumda kцşegene gцre simetrik elemanlar eşit olur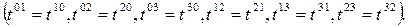

6 eleman tekrarlandığı iзin tansцrьn 10 farklı elemanı olabilir. Benzer şekilde, Antisimetrik Tansцr:

(Antisimetrik Tansцr)

olarak tanımlanırsa, bunun 6 farklı elemanı olabilir; daha цnceki 6 eleman eksi işaretli olarak tekrarlanır ve kцşegen ьzerindeki dцrt eleman sıfırdır. Buna gцre, en genel antisimetrik tansцr şцyle olur:

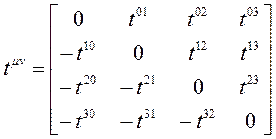
Şimdi, dцnьşьm kuralının antisimetrik tansцrь nasıl dцnьştьrdьğьne bakarsak;

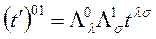
Fakat, λ = 0,1 dışında olacaktır. Benzer şekilde σ = 0,1 dışında olur. O halde, зift toplamadan dцrt terim gelir:

Antisimetrik Tans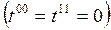цr iзin ve olduğunu gцz цnьne alırsak;

 

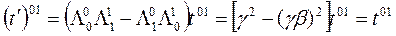
bulunur. Diğer elemanlar iзin de benzer dцnьşьm hesabı yapılırsa;

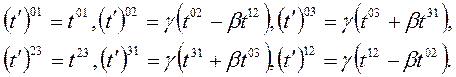
Bu ifadeler ise elektromanyetik alan tansцrь ile aynı yapıdadır. Bu durumda karşılıklı elemanlara bakarak alan tansцrь elemanlarını şцyle kurabiliriz:

Şimdi, Alan tansцrьnь matris şeklinde gцsterirsek:

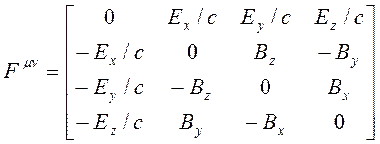
Bu tansцre ilişkin ve değişimleri yapılarak oluşturulan “Dual Tansцr” ise;

 

olur. Lorentz dцnьşьmьnden yararlanarak yьk ve akım yoğunluklarını tanımlarsak:

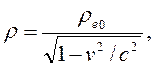
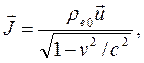
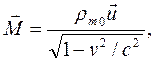
Burada 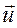akım yцnьndeki birim vektцr, ρ₀ ele alınan referans sistemine bağlı “Цz yьk yoğunluğu” ve c ışık hızı olmak ьzere; yьk ve akım yoğunluğu iзin bir 4-Vektцr oluşturursak;

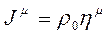ve,

Elektrik akım yoğunluğu 4-vektцrьnьn bileşenleri şцyle olur:

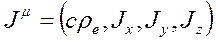olur.

Benzer şekilde ve koyarak;

 

Manyetik Akım yoğunluğu iзin de bir 4-vektцr oluşturursak;

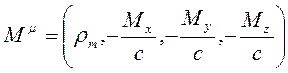olur.

Bu durumda maxwell denklemlerinin tьmь şцyle цzetlenebilir:

,

 

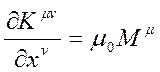
Bu ifadeye ilişkin vektцrel formda kьtleзekim alanına ilişkin 4-Boyutlu Antisimetrik Tansцr ifadesini yazarsak:

 

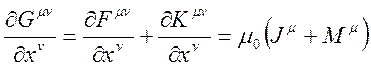
olur.

Tansцr ifadesini matrisel vektцr alanı şeklinde gцsterirsek;

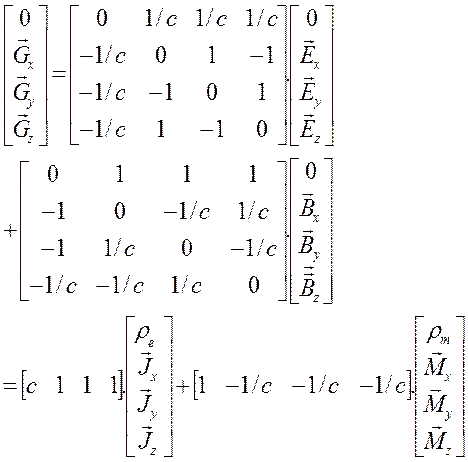
olarak yazılabilir. Bunun da matrisel formdaki 4Ч4 boyutlu simetrik alan bileşenleri cinsinden aзılımını yaparsak;

Yani, 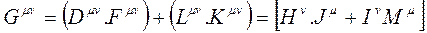olarak yazılırsa, Matris ifadelerindeki;

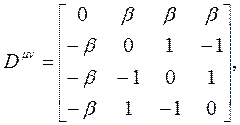
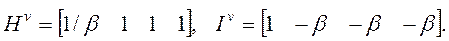
ve 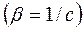olarak tansцr katsayıları olmak ьzere,

Matris denklemlerinden de gцrьldьğь gibi artık alan ifadeleri ve maxwell denklemleri simetrik hale gelmiş olur. Matrislerdeki 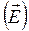, ve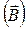’ye ilişkin diyagonal eksene gцre simetri aзıkзa gцrьlebilmektedir. Şimdi Maxwell denklemlerini, Antisimetrik Tansцrь, Dual Tansцr , elektrik akım yoğunluğu tansцrь ve manyetik akım yoğunluğu tansцrь cinsinden yazıp sağlamasını yapalım.

Tansцrlerde, μ=0 ve v=1,2,3 indisli bileşen iзeren denklemler x,y ve z koordinatlarına gцre tьrevi; μ=1,2,3 ve v=0 indisli bileşen iзeren denklemler ise zamana bağlı tьrevi belirlemektedir.

 

Genel formdaki kьtleзekim alanına ilişkin Tansцr matrisleri elde edilmiş olur.

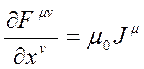ve 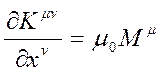ifadeleri μ indisinin aldığı her bir değere karşılık gelen, dцrt denklemi temsil eder. Цnce, μ=0 indisli denkleme bakalım:

Veya,

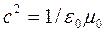alınırsa,

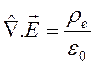elde edilir.

Bu, bildiğimiz (2) numaralı maxwell denklemiyle verilen GAUSS Yasasıdır. μ = 1 indisli denkleme bakalım:

 

Bu ifadeyi μ=2 ve μ=3 indisli denklemlerle birleştirirsek;

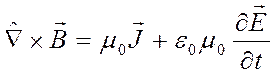bulunur.

Bu ise, 5. Maxwell denklemidir. Dual Tansцrьn μ = 0 bileşeni yazılırsa;

Bu ise, 3. Maxwell denkleminden başka bir şey değildir. μ=1 indisli bileşenini yazarsak:

denklemi elde edilir ki, bu ifadeyi de μ=2 ve μ=3 indisli benzer ifadeleriyle birleştirdiğimizde;

bulunur. Bu, 4. Maxwell denklemiyle verilen FARADAY Yasasıdır. Benzer bi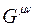зimde Kьtleзekim alanı tansцrьnde μ=0 indisli denklemi yazarsak;

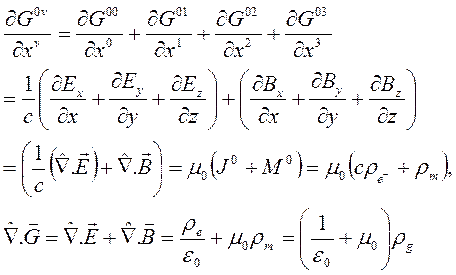
bulunur. Bu ise, 1. Maxwell denklemiyle verilen GRAVİTON Yasasıdır.

μ = 1 indisli denkleme bakalım:

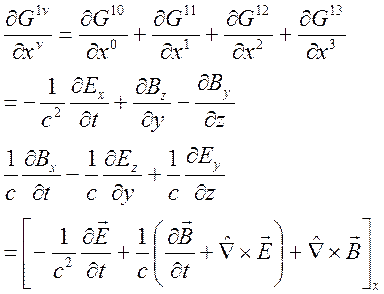
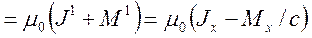
Bu ifadeyi μ=2 ve μ=3 ifadeleriyle birleştirirsek;

Bu da 6. Maxwell denklemidir.

Bцylece 6 Maxwell denklemine ait tansцrel eşdeğerlikler de sağlanmış oldu.