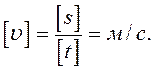Швидкість матеріальної точки

Нехай матеріальна точка m рухається по траєкторії АВ (рис. 2.2). Траєкторією точки називають послідовну сукупність положень її у просторі, тобто лінію, описувану точкою, що рухається. Якщо ця лінія пряма, рух називають прямолінійним, якщо лінія крива – криволінійним. Якщо всі точки ділянки траєкторії лежать в одній площині, то рух називають плоским. Якщо в момент часу t₁рухома точка m перебувала в положенні 1, а в момент часу t₂ – у положенні 2, то ділянка траєкторії

1a2 являє собою пройдений точкою шлях ∆S за час ∆t = t₂ – t₁.

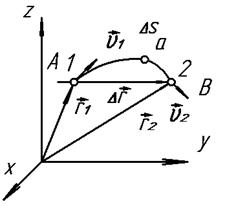
Рис. 2.2

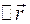Величину, рівну називають вектором перемі-щення (найчастіше просто переміщенням) точки за проміжок часу ∆t. Відношення переміщення до проміжку часу ∆t навивають середньою швидкістю матеріальної точки за час ∆t:

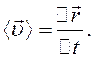(2.6)

При прямолінійному русі в одному напрямку 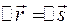, і

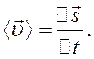(2.7)

На кожній малій ділянці траєкторії швидкість може бути різною. Тому при більш строгому вивченні руху зручніше користуватися поняттям миттєвої швидкості, яку називають просто швидкістю :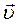

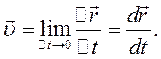(2.8)

З рівнянь (2.6) - (2.8) випливає, що швидкістю матеріальної точки може бути названа швидкість зміни положення цієї точки у просторі. При прагненні ∆t до нуля точка 2 наближається до точки 1, і швидкість 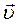спрямована по напрямку 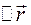, співпадає з дотичною до траєкторії, тобто в кожній точці траєкторії швидкість спрямована по дотичній до траєкторії. Крім того при 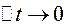отримуєм, що 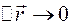, тоді випливає, що

i (2.9)

Швидкість центра інерції системи матеріальних точок визначається тим самим рівнянням (2.8).

Складові швидкості вздовж координатних осей описуються спів-відношеннями:

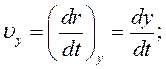
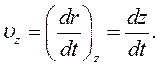(2.10)

Вектор швидкості і його модуль можна виразити через складові за рівняннями:

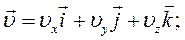
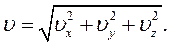(2.11)

Знаючи закон руху 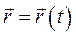, або 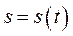, за рівняннями (2.8) і (2.9) можна вирішити пряме завдання – знайти швидкість, а також зворотнє – знайти 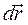і за деякий проміжок часу 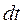:i 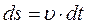. Для малого інтервалу часу ∆t справедливі співвідношення: . При нерівномірній швидкості на всій ділянці шляху між будь-якими двома точками можна одержати підсумовуванням окремих ділянок :

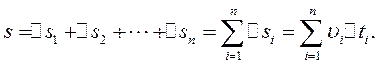
Остання рівність виконується тим точніше, чим менше інтервал ∆t_і. Точне виконання цієї рівності буде в межах при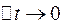

(2.12)

Аналогічно

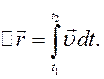(2.13)

За системою рівнянь (2.10) координати матеріальної точки в будь-який момент часу можна обчислити на підставі рівнянь:

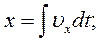
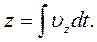(2.14)

Якщо закон руху розглядається після того, як точка пройшла вже деякий шлях 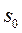, що відповідає переміщенню 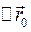і координатам , то рівняння (2.12) - (2.14) набирають виигляду:

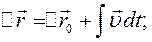
(2.15)

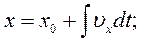
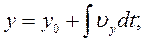
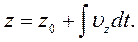
Нехай на початку відліку часу умовно нерухома система відліку K і система K', що рухається відносно K зі швидкістю 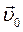, суміщені, а матері-альна точка m перебуває в початку відліку O. За деякий проміжок часу ∆t', виміряного у системі K', матеріальна точка m виконує переміщення 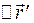(рис. 2.3) , а за такий самий проміжок часу ∆t, виміряний у системі K, сама система K' відносно K виконує переміщення 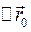. Переміщення точки m відносно системи K дорівнює: . Якщо прийняти, що час в обох системах відліку протікає однаково, 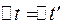, то швидкість матеріальної точки відносно системи K буде дорівнювати:

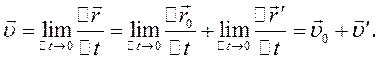(2.16)

Тут 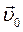– швидкість руху системи 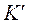відносно 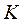, а 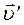– швидкість матеріальної точки m відносно системи 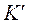. Рівняння (2.16) називають законом (або правилом) додавання швидкостей. Воно справедливе лише у випадку малих швидкостей у порівнянні зі швидкістю світла. При великих швидкостях рівність (2.16) не виконується, оскільки 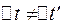. Рис. 2.3 Це коло питань розглядається в спеці- альній теорії відносності.

Розмірність швидкості можна отримати наоснові рівнянь (2.6) і (2.7):