Поле тяжіння
Закон всесвітнього тяжіння дає кількісну оцінку взаємодії, але не розкриває механізму тяжіння. Практика показує, що сила тяжіння не залежить від щільності навколишнього середовища. Таку взаємодію можна зрозуміти, якщо вважати, що всі тіла породжують навколо себе поле тяжіння (гравітаційне поле).
 Нехай деяке тіло з масою
Нехай деяке тіло з масою 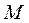 (рис. 8.4) утворює навколо себе гравітаційне поле. Розглянемо характеристики цього поля.Для цього по черзі будемо розміщувати тіла з масами
(рис. 8.4) утворює навколо себе гравітаційне поле. Розглянемо характеристики цього поля.Для цього по черзі будемо розміщувати тіла з масами  , Рис.8.4
, Рис.8.4 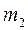 і
і 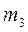 в точку простору, положення якої задано
в точку простору, положення якої задано
радіусом - вектором 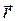 відносно тіла з масою
відносно тіла з масою 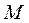 . З боку тіла з масою
. З боку тіла з масою 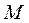 на кожне з тіл з масами
на кожне з тіл з масами  ,
, 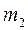 і
і 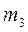 діють сили:
діють сили: 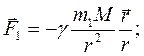
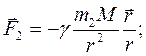

Розділивши сили 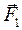 ,
,  і
і 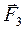 на маси
на маси  ,
, 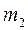 і
і 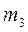 відповідно, отримаємо одну і ту ж величину:
відповідно, отримаємо одну і ту ж величину: 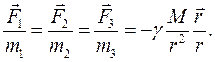
Це рівняння виражає силу, з якою гравітаційне поле діє на тіло з одиничною масою в заданій точці простору. Цю силу називають напруженістю поля тяжіння. Позначимо її через символ 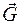 . Таким чином, напруженість поля тяжіння в певній точці простору виражається рівнянням:
. Таким чином, напруженість поля тяжіння в певній точці простору виражається рівнянням:
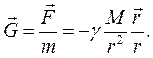 (8.14)
(8.14)
Напруженість поля є його силовою характеристикою.
Якщо напруженість поля в усіх його точках однакова за величиною і за напрямком, то поле називають однорідним.
Якщо в усіх точках поля його вектори напруженості спрямовані уз-довж прямих, які перетинаються в одній і тій же точці 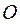 (рис. 8.5), нерухо-мій відносно обраної системи відліку, то поле називають центральним, а точку
(рис. 8.5), нерухо-мій відносно обраної системи відліку, то поле називають центральним, а точку  - центром сил.
- центром сил.
 Якщо чисельне значення напруженості поля залежить тільки від відстані
Якщо чисельне значення напруженості поля залежить тільки від відстані 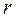 до центра сил
до центра сил 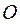 :
: 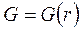 , то поле називають сферично симетричним. Очевидно, що поле тяжіння, створюване матеріальною точкою або однорідною кулею, є центральним і сферично симетричним.
, то поле називають сферично симетричним. Очевидно, що поле тяжіння, створюване матеріальною точкою або однорідною кулею, є центральним і сферично симетричним.
Якщо поле утворюється кількома (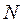 ) тілами, то напруженість сумарного поля дорівнює векторній сумі напруженостей полів, утворюваних кожним з тіл:
) тілами, то напруженість сумарного поля дорівнює векторній сумі напруженостей полів, утворюваних кожним з тіл:
Рис.8.5
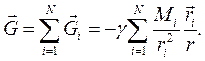 (8.15)
(8.15)
Це твердження називають принципом суперпозиції (накладання) полів, що є наслідком закону адитивності сил (рівняння (8.4)).
На підставі рівнянь (8.10) і (8.9) знаходимо, що прискорення віль-ного падіння тіла дорівнює напруженості поля тяжіння в тій точці, де в розглянутий момент перебуває тіло:
 (8.16)
(8.16)
Якщо тіло не вільне, то під дією поля тяжіння тіло діє на опору або підвіску із деякою силою 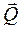 . Відповідно до третього закону Ньютона опора або підвіска діють на тіло із силою
. Відповідно до третього закону Ньютона опора або підвіска діють на тіло із силою 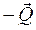 . Обидві ці сили викликають при-скорення тіла
. Обидві ці сили викликають при-скорення тіла 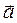 , а їх геометрична сума дорівнює сумарній силі, що діє на тіло:
, а їх геометрична сума дорівнює сумарній силі, що діє на тіло:
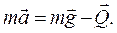 (8.17)
(8.17)
Сила 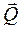 , з якою тіло діє на опору або підвіску:
, з якою тіло діє на опору або підвіску:
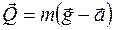 (8.18)
(8.18)
залежить від прискорення тіла разом з опорою або підвіскою.
Силу, з якою тіло, що перебуває в полі тяжіння, діє на опору або підвіску, називають вагою тіла. При цьому передбачається, що тіло, опора і підвіска будуть у тій системі відліку, в якій визначається вага. Коли говорять про вагу тіла, то, як правило, припускають, що тіло, опора і підвіс не мають прискорення відносно Землі. Отже, вага тіла, згідно з рівнянням (8.18), дорівнює силі ваги 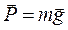 й залежить, строго кажучи, від положення цього тіла відносно Землі. Вагу тіла можна вважати постійною лише з тим ступенем наближення, з яким можна вважати постійним прискорення вільного падіння.
й залежить, строго кажучи, від положення цього тіла відносно Землі. Вагу тіла можна вважати постійною лише з тим ступенем наближення, з яким можна вважати постійним прискорення вільного падіння.
На підставі рівняння (8.18) знаходимо: якщо опора рухається вгору із прискоренням 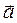 , то сила
, то сила 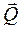 , з якою тіло діє на опору і опора на тіло, біль-ша від сили ваги (а значить, і ваги тіла) на величину
, з якою тіло діє на опору і опора на тіло, біль-ша від сили ваги (а значить, і ваги тіла) на величину 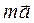 , що еквівалентно збільшенню ваги – тіло відчуває перевантаження. Рух опори вниз із приско-ренням
, що еквівалентно збільшенню ваги – тіло відчуває перевантаження. Рух опори вниз із приско-ренням 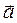 викликає зменшення сили
викликає зменшення сили 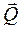 , що еквівалентно зменшенню ваги. При вільному падінні опори (
, що еквівалентно зменшенню ваги. При вільному падінні опори (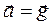 ) настає невагомість.
) настає невагомість.
Сили бувають консервативні, що проявляються в потенціальних по-лях, і неконсервативні, що проявляються в не потенціальних полях. З'ясуємо, до якої із цих категорій належать сили й поля тяжіння. Для цього знайдемо роботу сил поля з переміщення матеріальної точки т сила-ми тяжіння із точки 1 у точку 2 через проміжну точку 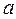 (рис. 8.6). Робота
(рис. 8.6). Робота 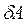 на елементарному переміщенні
на елементарному переміщенні  дорівнює:
дорівнює:  . Оскільки:
. Оскільки: 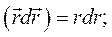 то
то
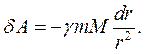 (8.19)
(8.19)
При переміщенні матеріальної точки 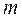 із точки 1 у точку 2 робота сил поля дорівнює:
із точки 1 у точку 2 робота сил поля дорівнює:
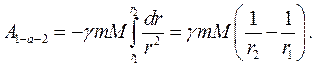 (8.20)
(8.20)
З рівняння (8.20) випливає, що робота  не залежить від форми траєкто-рії руху матеріальної точки т, а залежить лише від початкової й кінцевої відстаней між матеріальними точками т і М. Це означає, що
не залежить від форми траєкто-рії руху матеріальної точки т, а залежить лише від початкової й кінцевої відстаней між матеріальними точками т і М. Це означає, що  . Тоді:
. Тоді: 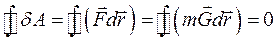
Отже, сили поля тяжіння, створюваного матеріальною точкою М, є консер-вативними, а розглянуте поле – потенціальним. На основі принципу адитив-ності сил тяжіння можна показати, що отриманий висновок справедливий і для кожного поля тяжіння, створюваного будь-якою сукупністю тіл.
У розділі V було показано, що робота  , яка виконується консер-вативними силами над системою, дорівнює зменшенню потенціальної енергії системи. У цьому випадку для матеріальної точки
, яка виконується консер-вативними силами над системою, дорівнює зменшенню потенціальної енергії системи. У цьому випадку для матеріальної точки 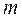 отримуємо:
отримуємо:
 (8.21)
(8.21)
Зіставляючи рівняння (8.20) і (8.21), знаходимо:
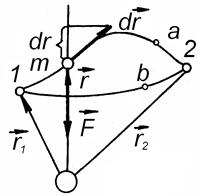
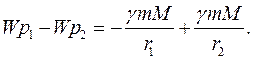
При прагненні 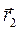 до нескінченності одержуємо:
до нескінченності одержуємо: 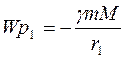 .
.
Оскільки точку 1 було обрано довільно, то в загальному випадку потенціальна енергія одно-го тіла в полі тяжіння, створюваного іншим ті-лом, може бути виражена рівнянням:
Рис.8.6 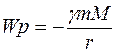 . (8.22)
. (8.22)
На основі принципу суперпозиції полів можна показати, що потен-ціальна енергія матеріальної точки з масою 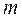 в полі тяжіння, створюва-ного сукупністю N матеріальних точок масами
в полі тяжіння, створюва-ного сукупністю N матеріальних точок масами 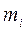 , дорівнює:
, дорівнює:
 . (8.23)
. (8.23)
Потенціальну енергію матеріальної точки з одиничною масою в даній точці поля називають потенціалом поля в цій точці:
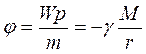 . (8.24)
. (8.24)
Якщо поле створюється сукупністю N матеріальних точок з масами 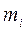 , то потенціал поля в обраній точці, згідно з рівняннями (8.23) і (8.24) дорівнює:
, то потенціал поля в обраній точці, згідно з рівняннями (8.23) і (8.24) дорівнює:
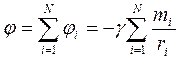 . (8.25)
. (8.25)
На підставі рівнянь (8.20), (8.21) та (8.24) знаходимо, що при 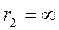
робота сил поля над тілом масою 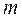
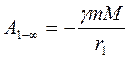 , а потенціал поля
, а потенціал поля
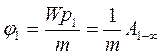 .
.
Це дає можливість надати фізичного змісту поняттям потенціальної енергії тіла в полі та потенціалу поля: потенціальна енергія тіла маси 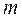 в довільно обраній точці потенціального поля кількісно дорівнює роботі сил поля по переміщенню цього тіла і цієї точки в нескінченність, а потенціал поля в довільно обраній точці кількісно дорівнює роботі сил поля по переміщенню тіла з одиничною масою із цієї точки в нескінченність. Якщо робота вико-нується зовнішніми силами проти сил поля, то її варто брати зі знаком „–”.
в довільно обраній точці потенціального поля кількісно дорівнює роботі сил поля по переміщенню цього тіла і цієї точки в нескінченність, а потенціал поля в довільно обраній точці кількісно дорівнює роботі сил поля по переміщенню тіла з одиничною масою із цієї точки в нескінченність. Якщо робота вико-нується зовнішніми силами проти сил поля, то її варто брати зі знаком „–”.
На підставі співвідношення 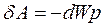 й рівняння (8.14) та (8.24) знаходимо:
й рівняння (8.14) та (8.24) знаходимо:
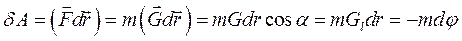 .
.
У загальному випадку потенціал поля може бути функцією координат і часу: 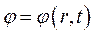 . Для стаціонарного поля, властивості якого в кожній точці простору з часом не змінюються, величина
. Для стаціонарного поля, властивості якого в кожній точці простору з часом не змінюються, величина  дорівнює:
дорівнює:  .
.
Тому: 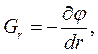
де 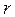 – довільний напрямок.
– довільний напрямок.
Проекції вектора 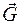 на координатні осі будуть рівні:
на координатні осі будуть рівні:

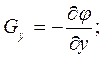
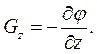
Вектор 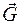 знайдемо, домноживши його проекції на відповідні орти:
знайдемо, домноживши його проекції на відповідні орти:
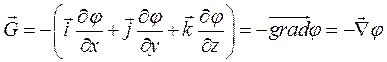 . (8.26)
. (8.26)
Рівняння (8.26) виражає зв'язок між напруженістю й потенціалом поля тя-жіння в довільно обраній точці.
Наведені тут положення теорії поля тяжіння можуть бути застосовані до тіл, що рухаються зі швидкостями, набагато меншими від швидкості світла в порожнечі. За великих швидкостей руху тіл треба застосовувати теорію поля тяжіння, яка базується на теорії відносності.