Розв’язати рівняння
ПРИКЛАДИ РОЗВЯЗАННЯ ДИФЕРЕНЦІЙНИХ РІВНЯНЬ:
1. Розв’язати рівняння:
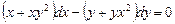 .
.
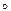 Оскільки це рівняння можна записати у вигляді
Оскільки це рівняння можна записати у вигляді
 ,
,
то воно є рівнянням з відокремлюваними змінними. Розділимо змінні:
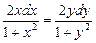 і проінтегруємо його
і проінтегруємо його 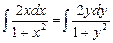 .
.
Отримуємо
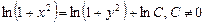 .
.
Потенціюючи, дістаємо загальний розв’язок рівняння:
 .
.
2. Розв’язати рівняння:
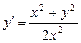 .
.
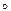 Дане рівняння перепишемо у вигляді:
Дане рівняння перепишемо у вигляді:
 .
.
Отже, рівняння є однорідним. Використаємо підстановку  , тоді рівняння буде
, тоді рівняння буде
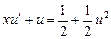 , або
, або 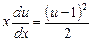 .
.
Відокремимо змінні
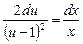 ;
; 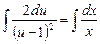 ;
; 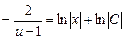 .
.
Загальний розв’язок рівняння буде
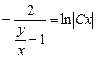 , або
, або  .
.
3. Знайти розв’язок рівняння  , що задовільняє початкову умову
, що задовільняє початкову умову  .
.
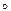 Дане рівняння є лінійним рівнянням першого порядку. Поклавши
Дане рівняння є лінійним рівнянням першого порядку. Поклавши  , матимемо:
, матимемо:
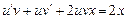 ;
; 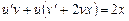 .
.
Отримаємо два рівняння:
1)  ; 2)
; 2) 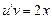 ;
;
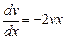 ;
; 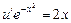 ;
;
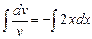 ;
; 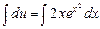 ;
;
 .
. 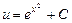 .
.
Загальний розв’язок даного рівняння
 .
.
Знайдемо значення стадої 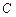 , при якому частинний розв’язок задовольняє задану початкову умому:
, при якому частинний розв’язок задовольняє задану початкову умому:
 , звідки
, звідки 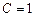 .
.
Отже,шуканий частинний розв’язок має вигляд 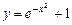 .
.
4.Розв’язати рівняння
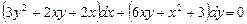 .
.
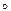 У даному випадку
У даному випадку

Оскільки
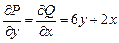 ,
,
то ліва частина заданого рівняння є повним диференціалом деякої функції  , причому
, причому
 (1)
(1)
Інтегруючи, наприклад, перше зцих рівнянь по 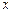 (вважаючи
(вважаючи  сталою), маємо
сталою), маємо
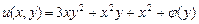 , (2)
, (2)
де 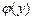 – довільна диференційовна функція
– довільна диференційовна функція  .
.
Диференціюючи рівність (2) по  , згідно з другим рівнянням (1), дістанемо
, згідно з другим рівнянням (1), дістанемо
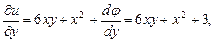
тобто 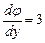 , звідки
, звідки  , тому
, тому
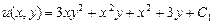 .
.
Отже, загальний інтеграл даного рівняння виражається рівністю
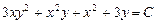 .
. 
5.Розв’язати рівняння
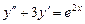 .
.
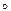 Покладемо
Покладемо 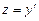 , тоді
, тоді 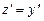 і маємо лінійне рівняння першого порядку відносно невідомої функції
і маємо лінійне рівняння першого порядку відносно невідомої функції 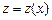 :
:
 .
.
Розв’язавши це рівняння, знайдемо 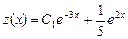 , тоді
, тоді 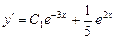 , звідки
, звідки
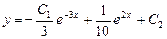 .
.
6.Розв’язати рівняння
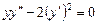 .
.
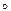 Поклавши
Поклавши
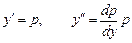 ,
,
дістанемо
 , або
, або 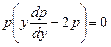 .
.
Це рівняння розпадається на два:
 .
.
З першого маємо  , звідки
, звідки 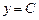 . У другому рівнянні відокремлюються змінні:
. У другому рівнянні відокремлюються змінні:
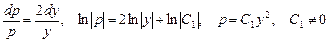 .
.
Оскільки 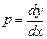 , то
, то
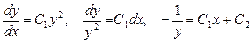 .
.
Звідси другий розв’язок рівняння буде:
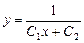 .
.
Отже,задане рівняння має два розв’язки
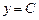 ,
, 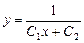 .
.
7.Розв’язати рівняння
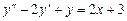 .
.
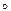 Загальний розв’язок даного рівняння будемо шукати в вигляді
Загальний розв’язок даного рівняння будемо шукати в вигляді 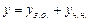 , де
, де  – загальний розв’язок відповідного однорідного рівняння,
– загальний розв’язок відповідного однорідного рівняння, 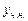 – частинний розв’язок неоднорідного рівняння.
– частинний розв’язок неоднорідного рівняння.
Характеристичне рівняння  має корені
має корені 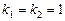 , тому загальний розв’язок однорідного рівняння має вигляд
, тому загальний розв’язок однорідного рівняння має вигляд 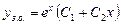 . Оскільки правою частиною даного рівняння є функція виду
. Оскільки правою частиною даного рівняння є функція виду 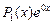 , причому
, причому 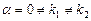 , то частинний розв’язок шукаємо в вигляді
, то частинний розв’язок шукаємо в вигляді  , тобто
, тобто  , де
, де  і
і  – невідомі коефіцієнти. Знайшовши похідні
– невідомі коефіцієнти. Знайшовши похідні  ,
,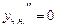 та підставивши їх у рівняння, маємо
та підставивши їх у рівняння, маємо
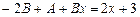 .
.
Прирівнюючи коефіцієнти при однакових степенях, дістаємо систему рівнянь
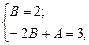
звідки 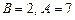 . Отже, частинний розв’язок даного рівняння має вигляд
. Отже, частинний розв’язок даного рівняння має вигляд  , тому
, тому
 –
–
шуканий загальний розв’язок.
8.Розв’язати рівняння
 .
.
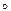 Характеристичне рівняння
Характеристичне рівняння  має корені
має корені 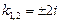 , тому загальний розв’язок однорідного рівняння має вигляд
, тому загальний розв’язок однорідного рівняння має вигляд  . Права частина даного рівняння
. Права частина даного рівняння 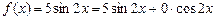 , де
, де 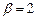 і число
і число 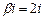 збігається з одним із коренів характеристичного рівняння, тому частинний розв’язок даного рівняння шукаємо у вигляді
збігається з одним із коренів характеристичного рівняння, тому частинний розв’язок даного рівняння шукаємо у вигляді 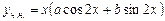 , де
, де  і
і – невідомі коефіцієнти. Знайшовши похідні
– невідомі коефіцієнти. Знайшовши похідні 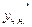 та
та 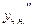 і підставивши
і підставивши 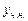 та
та 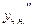 у вихідне рівняння, після спрощень дістанемо
у вихідне рівняння, після спрощень дістанемо
 .
.
Прирівнюючи коефіцієнти при  та
та  у лівій і правій частині цієї рівності, дістаємо систему рівнянь
у лівій і правій частині цієї рівності, дістаємо систему рівнянь
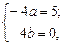
звідки  . Отже,
. Отже, 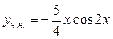 – частинний розв’язок даного рівняння, а загальний розв’язок буде
– частинний розв’язок даного рівняння, а загальний розв’язок буде
 .
.
9.Розв’язати рівняння
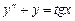 .
.
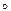 Характеристичне рівняння
Характеристичне рівняння 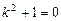 має корені
має корені  , тому загальний розв’язок однорідного рівняння має вигляд
, тому загальний розв’язок однорідного рівняння має вигляд 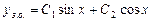 . Права частина
. Права частина  не єфункцією спеціального виду, тому частинний розв’язок даного рівняння методом підбору шукати не можна. Знайдемо цей розв’язок методом варіації сталої. Складемо систему виду:
не єфункцією спеціального виду, тому частинний розв’язок даного рівняння методом підбору шукати не можна. Знайдемо цей розв’язок методом варіації сталої. Складемо систему виду:

де 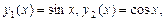 тоді система набуде вигляду:
тоді система набуде вигляду:
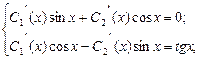
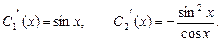
Інтегруючи дістанемо
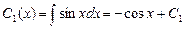 ;
;
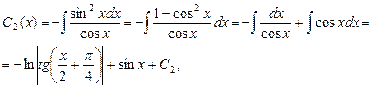
де  і
і 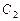 – довільні сталі. Отже, загальний розв’язок рівняння буде:
– довільні сталі. Отже, загальний розв’язок рівняння буде:
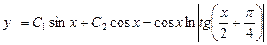 .
.
10.Розв’язати систему рівнянь

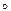 Продиференціюємо перше рівняння:
Продиференціюємо перше рівняння:
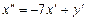 .
.
Підставимо в це рівняння значення похідної 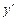 із другого рівняння системи:
із другого рівняння системи:
 .
.
Знайшовши з першого рівняння значення 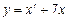 і підставивши його в знайдене рівняння, дістанемо
і підставивши його в знайдене рівняння, дістанемо
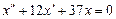 .
.
Маємо лінійне однорідне рівняння другог порядку з сталими коефіцієнтами. Інтегруючи його, одержуємо
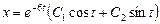 .
.
Оскільки 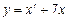 , то
, то
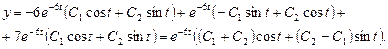
Отже, загальний розв’язок даної системи має вигляд:
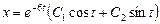 ,
,
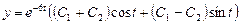 .
.