Лекция 2. Формирование и представление сигналов.

 

Нанесение информации на носители достигается определенным изменением па­раметров некоторых физических процессов, состояний, соединений, комбинаций эле­ментов. Чаще всего материализация информации осуществляется изменением парамет­ров физических процессов — колебаний или импульсных последовательностей. Подоб­ные операции называются модуляцией. Обратные операции восстановления величин, вызвавших изменение параметров при модуляции, называются демодуляцией.

Сигналами называются физические процессы, параметры которых содержат ин­формацию. Назначение сигналов заключается в том, чтобы в каком-либо физическом процессе отобразить события, величины и функции.

Для образования сигналов используются колебания (рис. 1.4 а) или импульсы

(рис.1.4 б ), которые рассматриваются как носители информации. В исходном состоянии эти носители представляют собой как бы чистую поверхность, подготовленную к нанесению необходимых данных — модуляции. По­следняя заключается в том, что изменяется какой-либо один или несколько (сложная модуляция) параметров носителя в соответствии с передаваемой информацией. Эти параметры будем называть информационными.

 

 

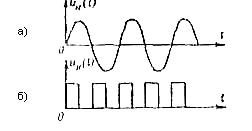
Рис.1.4 Виды носителей информации.

а - колебание; б - последовательность импульсов

 

Если обозначить параметры носителя через 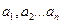, носитель как функция вре­мени может быть представлен в виде:

 

 

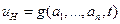
Модулированный носитель (сигнал) имеет вид:

 

 

Где — переменная составляющая параметра носителя, несущая информацию, или модулирующая функция. Последняя обычно связана с информационной (управляющей) функцией х линейной зависимостью:

 

 

Где 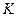— коэффициент пропорциональности.

Первый вид носителя — колебание (рис.1.4 а); например, переменное напряже­ние содержит три таких параметра: амплитуду , фазу , частоту (или период ).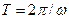

Второй вид носителя — последовательность импульсов (рис. 1.4 б) предоставля­ет еще большие возможности. Здесь параметрами модуляции могут быть: амплитуда импульсов , фаза импульсов 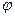, частота импульсов 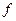, длительность импульсов или пауз 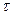, число импульсов 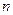и комбинация импульсов и пауз, определяющая код 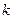. В последнем случае имеет место так называемая кодо-импульсная модуляция.

Для носителей первого типа различают следующие виды модуляции

AM — амплитудная модуляция (AM — amplitude modulation);

ЧМ — частотная модуляция (FM — frequency modulation);

ФМ— фазовая модуляция (РM — phase modulation).

Примечание. Частотную и фазовую модуляцию иногда совместно называют угло­вой модуляцией.

Для носителей второго вида:

АИМ – амплитудно-импульсная модуляция (PAM – pulse-amplitude modulation)

ЧИМ – частотно-импульсная модуляция (PFM – pulse-frequency modulation)

ВИМ – время-импульсная модуляция (PTM – pulse-time modulation)

ШИМ – широтно-импульсная модуляция (PDM – pulse-duration modulation)

ФИМ – фазоимпульсная модуляция (PPM – pulse phase modulation)

и другие.

Для того чтобы сигнал содержал информацию, он должен принципиально быть случайным. При описании сигнала некоторым количеством параметров часть из них может быть детерминированной, т. е. известной заранее, а часть случайной, т. е. несу­щей информацию. Часто представляет интерес изучение детерминированных характери­стик сигнала, и тогда можно условно говорить о детерминированном сигнале. Так, например, если сигналом служит импульс заранее известной формы и величины, то неизвестным заранее параметром является время его прихода; при этом о самом импуль­се можно говорить как о детерминированном сигнале.

При длительном существовании сигнала определенной формы последний также может рассматриваться на определенном интервале как детерминированный.

Случайный сигнал представляет собой модулированный носитель, у которого па­раметры являются случайными функциями времени. Случайный сигнал, у которо­го лишь небольшое число переменных параметров 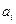, носит случайный характер, иногда называют квазидетерминированным.

Временная форма представления сигнала, т. с. описание его изменения или изме­нения параметров модуляции в функции времени, позволяет легко определить такие важные характеристики, как энергия, мощность и длительность сигнала. Однако суще­ствуют формы описания сигнала, лучше отображающие другие параметры.

Например, представление в виде ряда Котельникова дает возможность выделить некоррелированные интервалы.

Важнейшей характеристикой сигнала являются его частотные свойства. Для их исследования используется частотное представление функции в виде спектра, представ­ляющего собой преобразование Фурье временной формы.

В процессе обработки и передачи сигнала эта характеристика играет особую роль, так как определяет параметры используемой аппаратуры.

При рассмотрении спектров основных видов сигналов главное внимание уделяет­ся определению их ширины, поскольку в основном этот фактор используется для согла­сования сигнала с аппаратурой обработки информации (каналом): для исключения потери информации ширина спектра не должна превышать полосы пропускания канала.

Для периодического сигнала 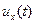спектр определяется соотношениями

 

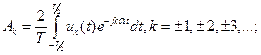(1.10)

 

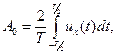(1.11)

 

где A_k — комплексный коэффициент ряда Фурье; А₀ — постоянная составляющая (среднее значение сигнала); Т— период сигнала: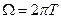— основная круговая частота, так что

 

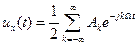(1.12)

 

Здесь А_к и А_{_к} являются комплексно-сонряжениыми величинами.

Функция (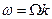, 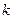пробегает все целые значения числовой оси от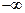

до 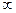) носит название комплексного спектра, ее модуль ||— амплитудного спектра сигнала 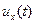, а зависимость фазы от частоты 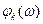- спектра фаз. Эти функции имеют решетчатый характер, так как они отличны от нуля только при целых значениях 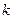. Таким образом, спектр периодической функции является дискретным. Его ширина 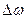определяется полосой положительных частот , на которой || имеет значимую величину. Вследствие сопряженности комплексных амплитуд их модули равны между собой:

 

 

Поэтому для представления спектра достаточно изобразить только положитель­ную полосу частот (рис.1.5 а). Дискретный спектр не обязательно означает периодич­ность функции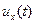. Последнее имеет место лишь в случае, когда расстояния между спектральными линиями |А_к| кратны основной частоте .

 

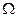Рис. 1.5 Спектры периодических и непериодических сигналов.

а — спектр периодического сигнала; б — спектр непериодического сигнала.

 

Для непериодического сигнала, определяемого на бесконечном интервале времени, преобразования Фурье имеют вид:

 

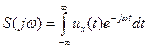(1.13)

 

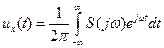(1.14)

 

Из сравнения (1.14) и (1.12) видно, что роль спектральной комплексной состав­ляющей сигнала па частоте выполняет бесконечно малая величина

 

 

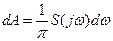
В связи с этим в случае непериодических функций рассматривается не спектр сигнала, а его производная по 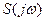носящая название спектральной плотности, или, как и в случае периодического сигнала, комплексного спектра; ее модуль |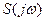| также называют спектром. Спектр непериодического сигнала имеет непрерывный характер

(рис.1.5 б). Ширина его 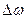определяется так же. как и для дискретного сигнала.

На рис. 1.6 представлены временная и частотная формы представления сигналов для невозмущенного гармонического носителя, амплитудно-модулированного сигнала и сигнала с угловой модуляцией.

 

 

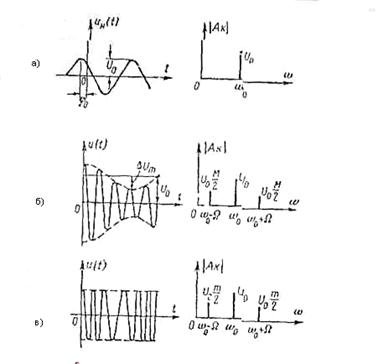
Рис. 1.6 Временная и частотная формы представления сигналов.

а - невозмущенный гармонический носитель;

б - амплитудно-модулированный сигнал;

в - сигнал с угловой модуляцией

 

Невозмущенный гармонический носитель можно записать в виде

 

 

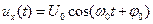
где — начальная фаза колебаний. Постоянная составлявшая отсутствует.

АМ-сигнал в общем виде описывается выражением

 

.

 

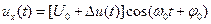Информацию переносит компонента.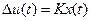

Если 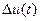представлена суммой гармонических колебаний, то

 

,

 

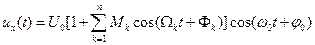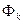где - частичные или парциальные, коэффициенты модуляции, представляющие от­ношения амплитуд высших гармоник к основной; и - частоты и фазы состав­ляющих .

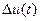Общий коэффициент модуляции есть наибольшее симметричное относительное отклонение 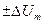амплитуды носителя от среднего значения :

 

 

Если 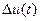представлено одним низкочастотным синусоидальным колебанием частоты 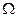, то

 

 

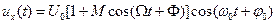
или

.

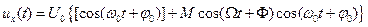Разлагая произведение косинусов

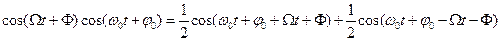
получаем:

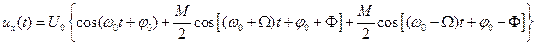
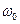
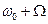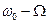Этим выявляются частотные составляющие и. Последняя формула позволяет построить диаграммы (рис. 1.6 б).

Более сложные модулирующие функции 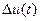раскладываются в ряд и анализи­руются аналогично. При этом на -диаграмме появляются дополнительные линии. Полная ширина полосы частот сигнала получается равной двойной ширине спектра модулирующей функции .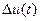

Рассмотрим теперь частотную и фазовую модуляции При изменении частоты все­гда меняется фаза колебаний, а при изменении фазы меняется частота. Этим определяет­ся общий характер частотной (ЧМ) и фазовой (ФМ) модуляций. Иногда их объединяют под общим названием угловой модуляции. ЧМ осуществляется прямым воздействием датчика на генератор для изменения частоты его колебании, хотя при переходах меняет­ся и фаза. При ФМ датчик воздействует на выходную цепь генератора, изменяя фазу несущего колебания, однако при переходах от одной фазы к другой меняется и частота колебаний. Особенно наглядно это видно (рис. 1.7) при скачкообразных изменениях и .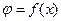

 

 

 

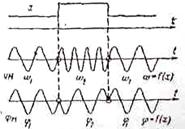
Рис. 1.7 Модуляция при скачкообразном изменении информационной функции

 

Здесь уместно напомнить некоторые соотношения для угловой частоты колеба­ния , частоты f в периодах, периода колебания Т и полной фазы колебания :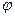

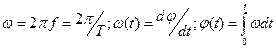
Из двух последних соотношений видно, что частоту можно оценивать по скоро­сти изменения фазы, а полную фазу (угол) — по интегральному значению угловой частоты.

Учитывая это обстоятельство, выражение для сигнала при произвольном измене­нии полной фазы можно записать в виде

 

 

При частотной модуляции частота носителя (процесса) отклоняется на от средней частоты 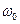в соответствии с информационной функцией х(t). Пусть модулирующая функция

Тогда угловая частота 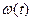носителя должна изменяться по закону

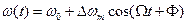
Если теперь использовать носитель в виде стабильного по амплитуде переменно­го напряжения

то, подставляя 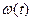из вышеприведенной формулы, получаем:

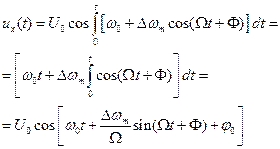
Максимальное отклонение 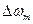, от 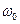называется девиацией частоты, а отноше­ние 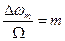—индексом модуляции. Используя последнее, перепишем:

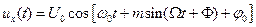(1.15)

В случае более сложной модулирующей функции, представляемой, например, ря­дом из косинусоидальных функций, частотно-модулированный сигнал будет описывать­ся выражением

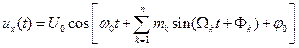(1.16)

Здесь 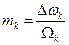— частичные, или парциальные, индексы модуляции, которые зависят от амплитуд и частот соответствующих гармоник.

При фазовой модуляции осуществляется сдвиг фазы носителя (процесса) на 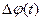от средней фазы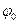. Если информация по-прежнему передастся элементарной косинусоидальной функцией, то

и фаза носителя изменяется по закону

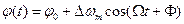
Следовательно, сигнал описывается выражением

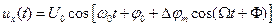
В случае фазовой модуляции также можно воспользоваться индексом модуляции, учитывая, что изменение частоты в пределах 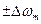, равносильно изменению фазы в пределах угла .

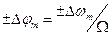Таким образом, индекс модуляции при ФМ равен девиации фазы

соответственно девиация частоты

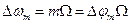
Текущее изменение фазы при ФМ

Полученное выше выражение для сигнала приобретает теперь вид:

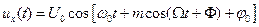(1.17)

Если информация передается суммой косинусоидальных функций, то ФМ-сигнал соответственно усложняется:

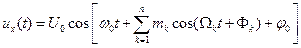(1.18)

где 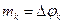— частичные, или парциальные, индексы модуляции, зависящие только от амплитуд гармоник.

Как показывают уравнения (1.15) и(1.17), при элементарной информационной функции постоянной частоте 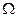сигналы ЧМ и ФМ трудно различимы. Однако, в случае ЧМ в сигнал 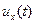входит интеграл информационной функци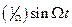и или 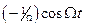, а в случае ФМ — сама функция 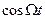или

 

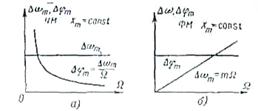
Рис. 1.8 Особенности частотно- и фазо-модулированных сигналов

а — случай частотной модуляции; б — случаи фазовой модуляции

 

При сложной информационной функции в виде суммы элементарных гармоник или при изменяющейся частоте элементарной функции различие между ЧМ и ФМ выявляется в полной мере.

Рассмотрим график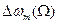и и 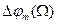для случаев ЧМ (рис. 1.8 а) и ФМ (рис. 1.8 б) Амплитуда информационной функции предполагается неизменной (х_m = const), поэтому 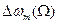при ЧМ и 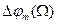при ФМ представлены горизонтальными линиями (они не зависят от частоты 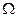). При ЧМ девиация фазы 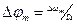убывает с увеличе­нием частоты 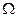информационной функции. При ФМ девиация частоты носителя пропорциональна частоте информационной функции.

Таким образом, медленной модулирующей функции при ЧМ соответствует очень большое отклонение фазы носителя, а при ФМ — малая девиация частоты носите­ля. Быстрой функции при ЧМ соответствует относительно малое отклонение фазы, а при ФМ - относительно большая девиация.

Для построения спектральных диаграмм необходимы дополнительные пре­образования.

Перегруппируем слагаемые в функции (1.15)

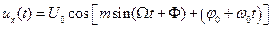
и разложим се по правилу косинуса суммы:

(1.19)

При индексе модуляции 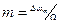много меньше единицы

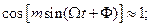
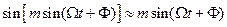
и полученное выражение запишется в виде

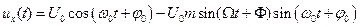
Но

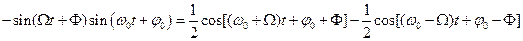
Тогда

(1.20)

Здесь вновь (как и в АМ, получаются три частоты - несущая, верхняя боковая 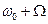и нижняя боковая 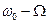; однако нижняя гармоника входит со знаком минус.

Для рассмотренного случая на рис. 1.6 в построены t-, -диаграммы. -диаграмма имеет одинаковый вид для ЧМ и ФМ и при малом m не отличается от АМ.

Однако при увеличении индекса модуляции частотный спектр ЧМ- пли ФМ-

сигнала сильно разрастается и по ширине превосходит спектр АМ-сигнала.

При общем анализе (для произвольного m) (1.19) разлагается в бесконечный ряд с коэффициентами, выражающимися через функции Бесселя. B этом случае в ЧМ- и ФМ- колебаниях даже при элементарной информационной функции 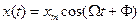обнаруживается бесконечный частотный спектр. Формула сигна­ла, записанная и форме ряда, имеет следующий вид:

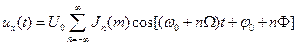
где— значение функции Бссселя первого рода порядка n для заданного m.

Таким образом, имеет место бесконечный линейчатый спектр с амплитудами гар­моник, пропорциональными

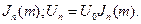Однако значения быстро убывают при увеличении n, начиная от n=m+1, и можно считать, что число боковых частот (с каждой стороны от 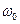) равно m+1. Ширина спектра равна при этом

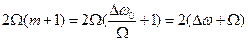(1.21)

 

 

 

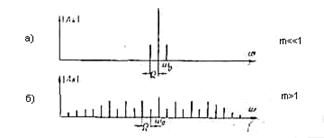
Рис. 1.9 Спектры ЧМ- и ФМ-сигиалон при различных индексах модуляции.