Некоторые нелинейные модели, сводящиеся к линейным

Основной задачей при определении вида математической модели исследуемого процесса является наиболее точное отображение общей тенденции зависимости Y от X. Общий вид математической модели представлен уравнением

Где 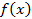– заранее неизвестная функция, подлежащая определению; 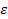- ошибка аппроксимации экспериментальных данных.

Наиболее простым решением поиска функциональной зависимости является линейный полином вида

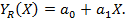
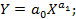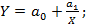Однако далеко не все зависимости можно описать полином первой степени. Существуют множество нелинейных функций, адекватных различным процессам и явлениям, например: степенная показательная гиперболическая логарифмическая 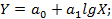экспоненциальная 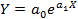и др.

Применение метода наименьших квадратов для определения коэффициентов регрессии нелинейных функций практически ничем не отличается от обычной схемы, следует лишь первоначально перед определением коэффициентов провести линеаризацию функции, т.е. привести нелинейные функции к линейному виду с помощью специальных преобразований.

Математические модели многих технологических процессов швейного производства и свойств текстильных материалов имеют нелинейный характер и представляют собой степенные, показательные, гиперболические и другие функции.

Выбор конкретного вида нелинейной зависимости можно проводить двумя методами:

· путем сравнения экспериментальной линии регрессии с характерными теоретическими кривыми для различных типов моделей;

· расчетным методом, определяя промежуточные значения входного и выходного факторов.

После определения вида нелинейной функции переходят к вычислению коэффициентов регрессии, используя операцию линеаризации.

Линеаризованное уравнение имеет вид уравнения прямой:

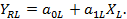
Существуют два вида нелинейности регрессионных моделей:

Нелинейные относительно независимых переменных.

Например,

.

В этом случае необходимо просто сделать замену переменных:

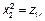
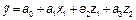
Нелинейные относительно параметров регрессии.

Например,

Выполним функциональное преобразование:

пусть 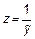тогда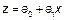

К сожалению, не всегда можно функциональными преобразованиями от нелинейных моделей перейти к линейным. Кроме того, нужно иметь в виду, что при вычислении параметров по методу МНК минимизируется сумма квадратов отклонений преобразованных, а не исходных данных.

Координаты промежуточных точек 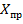и 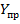, а также формулы для преобразования функции в линейный вид приведены в таблице

Функции, преобразованные в линейные

№, п/п	Вид модели, функция исходных переменных	Вид преобразования переменных и параметров	Вид уравнения прямой после преобразования	Координаты промежуточной точки исходных переменных
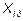
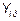
1.	Степенная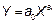
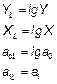
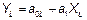
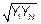
2.	Показательная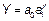
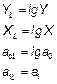
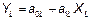
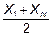
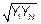
3.	Гиперболическая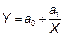
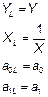
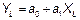
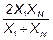
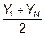
4.	Гиперболическая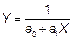
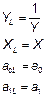
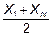
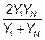
5.	Гиперболическая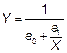
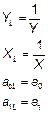
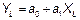
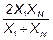
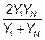
6.	Логарифмическая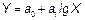
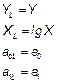
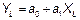
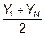
7.	Экспоненциальная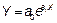

 

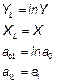
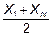
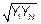
Промежуточное экспериментальное значение 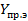, соответствующее 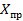, по формуле

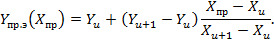
Определяют величины отклонений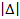

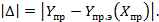
По величине минимального отклонения 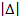определяют условный вид математической модели по табл., а также вид преобразований переменных и параметров - 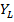, , 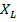, , 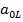вид уравнения прямой после преобразования.

Средний уровень линеаризованного фактора определяют по формуле

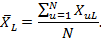
Определение коэффициентов регрессии

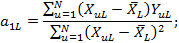
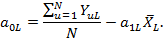
Вид линеаризованного уравнения находят, подставляя коэффициенты регрессии в формулу.

В линеаризованное уравнение подставляют непреобразованные переменные Y и X и определяют вид искомой математической модели.