Рототабельный ортогональный центрально-композиционный план

 

Рототабельный ортогональный центрально-композиционный план (РОЦКП) строится аналогично рассмотренному ранее ОЦКП. К использованному в качестве ядра плану ПФЭ 2ⁿ добавляются “звездные” точки - по две на каждый фактор и несколько точек в центре плана. “Звездные” точки должны располагаться на поверхности гиперсферы с радиусом R, на которой лежат и точки плана ПФЭ 2ⁿ, то есть величина плеча “звездных” точек 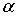должна равняться радиусу R. Это может быть обеспечено, при выполнении условия ортогональности, только при соответствующем выборе числа наблюдений в центральной (нулевой) точке плана n₀. Для РОЦКП n₀ зависит от числа факторов n. В ОЦКП n₀ = 1 для любого числа n.

Радиус сферы, на которой лежат точки плана ПФЭ 2ⁿ при двух уровнях варьирования факторов с диапазоном 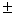1 составляет (рис. 38)

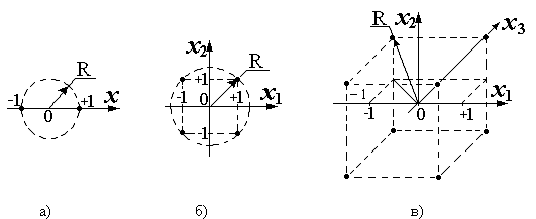
Рис. 38. Радиус окружности (сферы), на которой лежат точки плана ПФЭ 2ⁿ при диапазоне варьирования факторов от –1 до +1:

а) - n=1, ;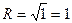

б) - n=2, ;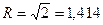

в) - n=3,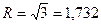

.

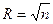Таким образом, при построении РОЦКП с ядром из плана ПФЭ 2ⁿ плечо “звездных” точек определяется числом факторов

.

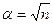Раннее при определении параметров ортогонального композиционного плана второго порядка с ядром из плана ПФЭ 2ⁿ было получено

,

где 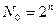- число точек плана ПФЭ,

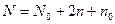- полное число точек композиционного плана второго порядка,

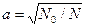- константа преобразования элементов столбцов, соответствующих квадратам факторов.

В этом случае для РОЦКП число наблюдений в центре плана

.

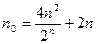Если n₀ не целое, то при практическом построении плана его округляют до целого, но свойство ортогональности плана нарушается.

Параметры РОЦКП в зависимости от числа факторов

n
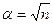
		1,414	1,732		2,236	2,45	2,646	2,83
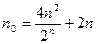
			10,5		13,13	14,25	15,53
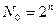
N			24,5		55,13		157,55
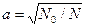
	0,5	0,5	0,574	0,67	0,76	0,84	0,9	0,94

 

В [1] без вывода для РОЦКП рекомендуется принимать

.

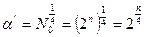Тогда

.

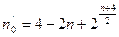Параметры РОЦКП по [1]

 

 

N
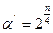
	1,189	1,414	1,682		2,378	2,838	3,364
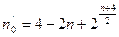
	7,66		9,31		16,63		33,25
N'	11,66		23,31		58,63		177,25
a'	0,414	0,5	0,586	0,57	0,739	0,8	0,85	0,889

 

В некоторых случаях ортогональное планирование второго порядка не отвечает потребностям практики – при описании поверхности отклика, особенно в окрестностях точки оптимума, более значимой является оценка дисперсии уравнения в целом, чем оценка дисперсии отдельных коэффициентов полинома. В этом случае обычно стремятся к равномерности распределения информации в уравнении функции отклика по всем направлениям. Такому положению отвечают ротатабельные планы. Кроме сказанного, подобные планы второго порядка позволяют минимизировать систематические ошибки, связанные с неадекватностью представления результатов полиномами второго порядка. Но построение ротатабельного плана второго порядка более сложно, чем ортогонального, а сама задача построения не имеет однозначного решения. Один из подходов к построению таких планов состоит в следующем.

Путем специального подбора звездного плеча g ЦКП Бокса можно сделать ротатабельным, иначе говоря, ЦКП Бокса можно сделать или ортогональным или ротатабельным.

Точки ротатабельного ЦКП Бокса второго порядка располагают на концентрических гиперсферах, количество которых не менее двух. Первая гиперсфера может быть вырожденной, т. е. представлять собой центральную точку плана, ее радиус r₁ = 0. Именно такая сфера часто используется на практике.

Вторая гиперсфера соответствует вписанному в нее кубу, выбранному в качестве ядра плана. Для ядра х_i = 1, следовательно, радиус этой гиперсферы

r₂ = (х₁² + х₂² + … + х_k²)^1/2 = (k)^1/2.

Ядро представляет собой ПФЭ вида 2^k или ДФЭ вида 2^{k – p} , причем должно соблюдаться условие (k – p)/4 > 3/4. Следовательно, с учетом ограничений на ЦКП Бокса, если k ³ 5, то в качестве ядра можно использовать полуреплику, если k ³ 8, ядром может служить четверть реплика.

Третья гиперсфера имеет радиус r₃ = 2 ^{k / 4} для ядра в виде ПФЭ и радиус r₃=2^(k-p)/4 для ядра в виде ДФЭ.

Таким образом, каждый фактор в ротатабельном ЦКП Бокса варьируется на пяти уровнях. В некоторых случаях радиусы второй и третьей гиперсферы совпадают:

n = 2:

r₂ = 2 ^1/2, r₃ = 2 ^2/4 = 2^1/2;

n = 8 и p = 2:

r₂ = 8 ^1/2 = 2 ^3/2, r₃ = 2 ^{(8 – 2)/4} = 2^3/2.

Коэффициенты модели и их дисперсии рассчитываются на основе использования обратной матрицы по формулам [Ас]:

;

; ;

;

;

;

;

;

;

.

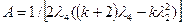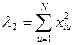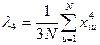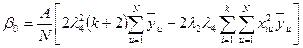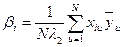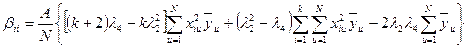
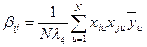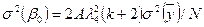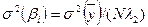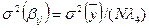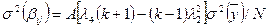Представленные формулы справедливы для ротатабельного планирования при любом количестве независимых переменных. Такое планирование не позволяет получить независимые оценки для всех коэффициентов модели, коррелированными оказываются коэффициенты (b₀, b_ii) и (b_ii, b_ij). Взаимную связь этих пар коэффициентов можно охарактеризовать ковариациями:

cov(b₀, b_ii) = – 2s²(ỹ) l₄ A/N ;

cov(b_ii, b_ij) = s² (ỹ) (1–l₄ )A/N.

Если повторные наблюдения имеются только в центре плана, то

 

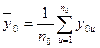
и величина

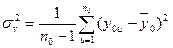
будет несмещенной оценкой дисперсии ошибок наблюдения. При ненасыщенном планировании остаточная сумма

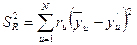
отличается от нуля. Здесь – величина, предсказанная уравнением модели, – найденная экспериментально. Величина

s_R² =S_R / [N–(k+1)(k+2)/2]

характеризует неадекватность модели и также является несмещенной оценкой дисперсии ошибок наблюдения.

На основании рассчитанных величин можно провести все необходимые проверки коэффициентов и модели в целом.

Иногда интерес представляет информация о функции отклика в некоторой окрестности центра плана. В этом случае следует добиться одинаковой погрешности модели внутри гиперсферы единичного радиуса. План, обеспечивающий такое свойство функции отклика, называется униформ-ротатабельным. Для его формирования достаточно обеспечить равенство дисперсии в центре плана (r = 0) и на поверхности гиперсферы радиуса r = 1. Этого добиваются подбором числа наблюдений n₀ в центре плана, а именно параметр λ₄ следует взять равным положительному корню квадратного уравнения

2λ₄ (λ₄ – 1)(k + 2) + λ₄ (k + 1) – (k – 1) = 0.

Рассмотренное композиционное планирование представляет собой один из возможных подходов к построению ротатабельных планов второго порядка.