Композиционные планы
Применение линейных планов совместно с методом градиентного поиска оптимума позволяет достичь окрестностей точки оптимума. Поиск оптимального решения в этой области требует перехода от линейных моделей к моделям более высокого порядка – как минимум к полиномам второй степени. Полиномы второго порядка содержит
 .
.
эффектов:
 , j>i. (5.1)
, j>i. (5.1)
Построение такой модели требует применения плана, в котором каждая переменная принимает хотя бы три различных значения. Существуют различные подходы к построению планов второго порядка. Можно воспользоваться ПФЭ типа 3k, но такие планы обладают большой избыточностью. Например, для трех переменных количество точек плана составит 27, а количество оцениваемых коэффициентов в функции отклика равно 10. В соответствии с идеей пошагового эксперимента планирование рационально осуществлять путем добавления специально подобранных точек к “ядру”, образованному планированием для линейного приближения. Такие планы называют композиционными (последовательными), они позволяют использовать информацию, полученную в результате реализации линейного плана.
Композиционные планы используются обычно на заключительном этапе исследования, когда модель приходится подбирать последовательно, начиная с простейшего линейного уравнения, которое потом достраивается до полной квадратичной формулы. В этом случае композиционные планы дают выигрыш по числу опытов по сравнению с другими планами. Эти планы можно применять и при непосредственном построении функции отклика в виде полинома (5.1).
Решение подобных задач основано на применении ортогональных или ротатабельных центральных композиционных планов (ЦКП). Эти планы используют в качестве ядра полный факторный эксперимент или минимально возможные регулярные дробные реплики типа 2k–p. В качестве дробной реплики применяют такую, в которой два любых парных взаимодействия по модулю не равны друг другу
 (5.2)
(5.2)
для любых попарно различных индексов. Именно план ПФЭ или дробные реплики, удовлетворяющие указанному условию, служат ядром ЦКП. На практике широкое распространение получили два типа ЦКП, известные как планы Бокса и Хартли. Понятие “центральный” означает, что факторы принимают значения, симметричные относительно центра плана.
Центральный композиционный план второго порядка называют планом Бокса, если его ядром является ПФЭ 2k или регулярная реплика типа 2k – p, для которой парные взаимодействия не равны по модулю линейным факторам:
xi ≠ ±xsxz; s ≠ z; i, s, z = 1, 2, …, k
и, кроме того, выполняется условие (5.2). Применение ПФЭ или регулярных реплик, отвечающих этим условиям, позволяет получить несмещенные оценки коэффициентов модели (5.1). Из условий построения дробной реплики следует, что разрешающая способность ядра плана должна быть больше четырех, т.е. определяющий контраст должен содержать не менее пяти переменных. Следовательно, ядром плана Бокса при k < 5 является ПФЭ, а при k ³ 5 может быть ДФЭ.
План Бокса можно сделать ортогональным либо ротатабельным. Но нельзя добиться одновременного и строго соблюдения обоих свойств. В некоторых случаях ЦКП можно сделать приближенно и ортогональным, и ротатабельным, если вначале построить ротатабельный план, а затем подобрать необходимое количество опытов в центральной точке.
Центральный композиционный план второго порядка называют планом Хартли, если его ядром является регулярная реплика типа 2k–p, в которой некоторые парные взаимодействия равны по модулю линейным факторам. Иначе говоря, ЦКП второго порядка будет или планом Бокса или планом Хартли. Планы Хартли обычно более экономны по числу опытов, чем планы Бокса, но уступают им по точности оценивания коэффициентов, кроме того, их нельзя сделать ни ортогональными, ни ротатабельными. Планы Хартли целесообразно применять, если известно, что часть эффектов bj или bju в модели отсутствует (следовательно, простые эффекты можно смешивать с парными взаимодействиями, не теряя в разрешающей способности плана) или тогда, когда дисперсия наблюдений относительно мала.
5.9.2. Композиционные планы типа Вn
Планы типа Вn представляют собой симметричные планы второго порядка с ядром в виде ПФЭ 2k или ДФЭ 2k–p, дополненные 2k звездными точками с плечом g =1 и опытами в центре плана. Иначе говоря, эти планы состоят из 2k (2k–p) вершин k-мерного гиперкуба с координатами ±1, из 2k центров (n–1)-мерных граней и некоторого числа опытов в центре гиперкуба. Количество точек плана с ядром из ПФЭ составляет N = 2k + 2k +1 (для ДФЭ N = 2k–p + 2k +1) при числе точек в центре гиперкуба равном единице. В каждой точке проводится равное число опытов. Планы этого типа имеют минимально количество уровней варьирования факторов, равное трем, что позволяет более точно выдерживать режимы работы изделий при натурных испытаниях по сравнению с планами, в которых требуется большее число уровней изменения управляемых переменных. Планы типа Вn близки к D- и G- оптимальным планам.
Обычно результаты опытов в нулевой точке служат для проверки гипотезы об адекватности модели экспериментальным данным. Если оценку параметров выполнять по результатам опытов в звездных точках и точках ядра, то [2]
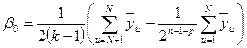 ;
;
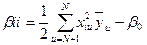 ;
;
 ;
;
 ,
,
где N1 – число точек ядра плана; – среднее значение отклика в u-й точке, полученное по r опытам. Если некоторые коэффициенты незначимы, то остальные уточняются по специальным формулам.
5.10. Планы для оценки влияния факторов.
Планы на латинских квадратах
При составлении планов поиска оптимальных значений функции и описания поверхности отклика предполагалось, что факторы представляют собой непрерывные величины. Однако некоторые параметры систем носят дискретный характер и принимают только относительно небольшое количество значений, например, емкость запоминающих устройств, тактовая частота системной шины персонального компьютера. Другие факторы по своей природе имеют не количественную, а качественную природу, в частности, однотипные изделия выпускаются целым рядом изготовителей. Этим изделиям можно приписать некоторые обозначения в номинативной шкале измерений.
Таким образом, существует параметры (характеристики), принимающие некоторое ограниченное количество значений, задаваемых в количественной или качественной шкале измерений. Необходимо в условиях воздействия других факторов оценить влияние таких параметров на показатель качества системы или определить их значимость. Полный перебор возможных сочетаний параметров системы потребует чрезмерно большого количества опытов. С целью рационального сокращения экспериментальных исследований применяют специальный вид планов – планы на латинских квадратах.
Латинский квадрат характеризуется особым расположением некоторого числа символов в ячейках, сгруппированных в строки и столбцы так, что каждый символ встречается один раз в каждой строке и в каждом столбце.
Латинским квадратом называется квадратная матрица размерности ( ), элементами которой являются латинские буквы. При этом каждая из n букв в каждом столбце и в каждой строке встречается один раз.
), элементами которой являются латинские буквы. При этом каждая из n букв в каждом столбце и в каждой строке встречается один раз.
 или
или 
Если по диагонали квадрата идет одна и та же буква, то латинский квадрат называется каноническим.
Латинские квадраты используются для кодирования уровней качественного фактора.
При планировании латинский квадрат используется в рандомизированном виде, т.е. его строки и столбцы расположены случайным образом.
Греко-латинский квадрат.
Греко-латинский квадрат используется в случае, если число качественных факторов равно двум. Это тоже квадратная  матрица, элементами которой являются две буквы - одна латинская, другая греческая. В греко-латинском квадрате комбинация греческой и латинской буквы встречается всего один раз.
матрица, элементами которой являются две буквы - одна латинская, другая греческая. В греко-латинском квадрате комбинация греческой и латинской буквы встречается всего один раз.
Латинский квадрат Греческий квадрат


Объединив данные латинский и греческий квадраты, мы не получим греко-латинского квадрата:
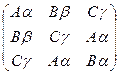
Поменяв местами вторую и третью строки греческого квадрата и объединив полученные латинский и греческий квадраты, получим греко-латинский квадрат:

Пример латинского квадрата, размером n×n, для n = 3 представлен в табл. 6.1.
Таблица 6.1
| a | b | c |
| b | c | a |
| c | a | b |
Для любого n > 2 существует множество вариантов построения латинских квадратов. Количество вариантов латинских квадратов с ростом n быстро увеличивается и определяется формулой
N(n, n) = n!( n – 1)!L(n).
Некоторые значения L(n) представлены в табл. 6.2.
Таблица 6.2
| n | ||||||
| L(n) |
Латинскому квадрату можно сопоставить план эксперимента, в котором строки соответствуют различным значениям одного фактора, столбцы – значениям другого, а латинские буквы – значениям третьего фактора, т.е. латинский квадрат позволяет исследовать влияние не более чем трех факторов. Пример представления латинского квадрата для факторов L, P, Z, каждый из которых варьируется на четырех уровнях (n = 4) приведен в табл. 6.3.
Таблица 6.3

| 
| 
| 
| |

| 
| 
| 
| 
|

| 
| 
| 
| 
|

| 
| 
| 
| 
|

| 
| 
| 
| 
|
Применение плана, построенного на основе латинского квадрата, позволяет оценить дифференциальный (разностный) эффект пар уровней, но не дает информации о взаимодействии между факторами (иначе говоря, факторы не зависят друг от друга). Так, сумма результатов экспериментов, соответствующих столбцу j, будет оценивать эффект Pj, усредненный по всем L и Z. Тогда дифференциальный эффект увеличения значения фактора P от уровня 1 до уровня 2, усредненный по всем L и Z, можно оценить по разности между суммой значений функции отклика столбца 2 и столбца 1. Порядок перечисления уровней факторов роли не играет.
В условиях применения латинского квадрата все факторы должны варьироваться на одинаковом количестве уровней. Можно ослабить это требование путем приравнивания какого-либо уровня другому.
Приведенный пример является одним из возможных расположений уровней факторов, позволяющих получить несмещенные оценки главных эффектов. Латинские квадраты можно накладывать друг на друга, образуя греко-латинские квадраты. Например, два латинских квадрата 3´3 можно преобразовать в греко-латинский квадрат.
Здесь латинские буквы образуют один латинский квадрат, а греческие буквы – другой латинский квадрат. Каждая латинская буква встречается в паре с конкретной греческой буквой только один раз. С помощью греко-латинского квадрата можно оценить главные эффекты четырех 3-х уровневых факторов (фактора строк, фактора столбцов, римских букв и греческих букв) проведя только 9 опытов.
Если наложить друг на друга три различных варианта латинских квадратов, то получится план гипер-греко-латинского квадрата. С его помощью можно оценить главные эффекты пяти факторов (фактора строк, столбцов и трех расположений квадратов). В частности, для пяти трехуровневых факторов потребуется провести только 9 опытов вместо 243 опытов при переборе всех возможных сочетаний факторов.
Гипер-греко-латинский квадрат используется, когда число качественных факторов равно трем. Это тоже квадратная матрица, каждый элемент которой состоит из греческой буквы, латинской буквы и цифры. Основным признаком является то, что каждая комбинация во всей матрице встречается один раз.
Итак, планы латинских (греко-латинских) квадратов используются в тех случаях, когда требуется оценить влияние факторов, варьируемых более чем на двух уровнях и заранее известно, что между факторами нет взаимодействий или этим взаимодействиями можно пренебречь. Имеются таблицы латинских и греко-латинских квадратов различных размеров, за исключением одного практически важного случая – не существует греко-латинского квадрата для 6 уровней факторов.