Планы для экспериментирования в условиях дрейфа
Блочные планы, ортогональные к дискретному дрейфу, представляют собой обычные планы типа ПМА, сбалансированные так, чтобы часть столбцов плана использовалась для оценки эффектов дискретного дрейфа независимо от эффектов исследуемых факторов.
Планы, ортогональные к непрерывному дрейфу, могут быть построены на основе таблиц полиномов Чебышева. Они используются для изучения линейных эффектов управляемых количественных факторов независимо от полиномиального дрейфа любого порядка. В случае необходимости оценки также и взаимодействий управляемых факторов используют обычные планы 2*, отбирая те столбцы планов, которые имеют минимальные корреляции с эффектами дрейфа. К этим же планам относятся планы Кокса, предназначенные для изучения одной количественной или качественной переменной, варьируемой на двух, трех, четырех уровнях в условиях дрейфа второго и третьего порядков.
Комбинированные планы для совместного изучения количественных и качественных переменных в условиях непрерывного полиномиального дрейфа получают соответствующим комбинированием планов Чебышева и планов Кокса.
Планы для экспериментирования в условиях дрейфа используются для исключения влияния неоднородностей типа дискретного и непрерывного дрейфа на исследуемые эффекты и оценки этого влияния независимо от эффектов варьируемых факторов и составляют основу группы планов ковариационного анализа.
Факторный эксперимент при изучении смесевых систем
Введение. Задача факторного эксперимента при изучении смесевых систем не отличается от задачи факторного эксперимента второго порядка, изложенной в 1.6. Однако при изучении свойств смесей, зависящих только от соотношений компонентов, желательно учитывать условие
 , (2.1)
, (2.1)
где xi – относительные концентрации компонента (хi 0); п – количество компонентов (n
0); п – количество компонентов (n 2).
2).
Условие (2.1) не позволяет использовать планы ПФЭ и модели типа (1.97) – матрица (ХТХ)-1 оказывается вырожденной.
Шеффе ввел каноническую форму полинома степени п:
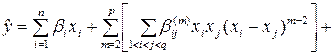
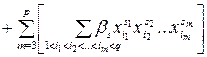 . (2.2)
. (2.2)
где
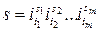 ;
; 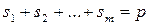 .
.
Наиболее часто пользуются следующими приведенными (каноническими) полиномами:
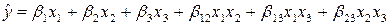 (2.3)
(2.3)
- полином второго порядка для трехкомпонентной смеси;
 (2.4)
(2.4)
- полином неполного третьего порядка для трехкомпонентной смеси;
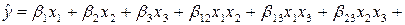
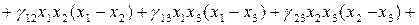
 (2.6)
(2.6)

– полином четвертого порядка для трехкомпонентной смеси.
Пояснение. От стандартного полинома, например, второго порядка
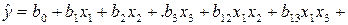
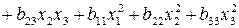 (2.7)
(2.7)
к полиному Шеффе (2.3) переходят путем несложных преобразований условия

в условия
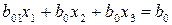 ;
;
 ;
;
 ; (2.8)
; (2.8)
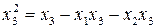 ;
;
и подстановкой (2.8) в (2.7). Получают
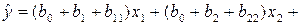
 (2.9)
(2.9)
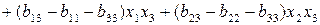 .
.
Симплекс-решетчатые планы Шеффе. Известно, что геометрическое место точек, удовлетворяющее условию (2.1), представляет собой п-1 правильный симплекс. Тогда факторное пространство может быть представлено симплексами с такой же системой координат. Планирование на симплексах осуществляется равномерным разбросом экспериментальных точек. Получаются {п, m} – решетки, где п – число компонентов смеси; т – порядок полинома. Примеры {3, т} – решеток с принятыми обозначениями выходной переменной приведены на рис. 2.1.
Симплекс-решетчатые планы частично композиционные. Неполную кубическую решетку {3, 3*} (рис. 2.1, б) можно получить из {3,2} (см. рис. 2.1,а) добавлением одной точки в центре симплекса; решетку {3, 4} (см. рис. 2.1, г) – добавлением точек к решетке {3, 2} (см. рис. 2.1, а).
2.1.1. Алгоритм симплекс-решетчатых планов второго порядка для трехкомпонентной смеси. Исходные данные. Имеется трехкомпонентная смесь. Необходимо получить зависимость некоторого свойства у от состава смеси в виде (2.3) и проверить ее адекватность.
План эксперимента для рассматриваемого случая приведен в табл. 2.1.
В каждой точке решетки проводится одинаковое число (т) параллельных опытов.
Расчет коэффициентов уравнения. Расчет коэффициентов возможен методом наименьших квадратов по уравнению 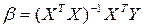 .
.

Рис. 2.1 {3, т} – симплексные решетки для полинома порядка:
а – второго; б – неполного третьего; в – третьего; г – четвертого.
Таблица 2.1 План эксперимента
| Номер опыта | План | Выходная переменная | ||||||
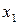
| 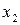
| 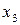
| 
| 
| … | 
| 
| |
| 0,5 0,5 | 0,5 0,5 | 0,5 0,5 | 
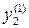
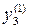
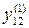


| 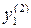



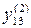

| ... … … … … … | 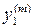


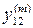
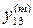
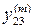
| 
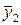
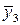


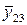
|
Однако, учитывая, что план эксперимента насыщен (число неизвестных коэффициентов равно числу уравнений), несложными преобразованиями можно получить следующие расчетные уравнения:
 ,
, 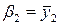 ,
, 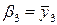 или
или  ; (2.10)
; (2.10)
 , например,
, например,  . (2.11)
. (2.11)
Проверка адекватности уравнения. Учитывая, что план эксперимента насыщенный, проверка адекватности по критерию Фишера (см. (1.92) – (1.96)) невозможна. Для проверки адекватности необходимо, выбрать несколько дополнительных точек плана, провести в них эксперимент и изучить разность между экспериментальным значением и полученным по уравнению. Эти точки выбирают либо в интересующей исследователя области, либо в точках, которые можно использовать для построения полинома более высокого порядка. Для получения дисперсии адекватности можно применять уравнение остаточной суммы
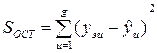 ;
; 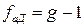 , (2.12)
, (2.12)
где уэи – экспериментальные значения выходной переменной в дополнительных проверочных точках; 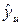 – значения выходной переменной для условий Хэ проверочных точек, полученных по уравнению; g – число проверочных точек;
– значения выходной переменной для условий Хэ проверочных точек, полученных по уравнению; g – число проверочных точек; 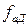 – дисперсия адекватности.
– дисперсия адекватности.
Если g>2, то адекватность можно проверять по критерию Фишера (см. (1.94), (1.95), а ошибку опыта 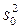 при равном числе параллельных опытов т рассчитать по формулам (1.138) – (1.141) (условие однородности дисперсий также необходимо проверять).
при равном числе параллельных опытов т рассчитать по формулам (1.138) – (1.141) (условие однородности дисперсий также необходимо проверять).
Если адекватность уравнения оценивается по одной проверочной точке, то удобнее пользоваться уравнениями, приведенными ниже (их доказательство в [5]). Для оценки используется t-критерий:
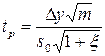 , (2.13)
, (2.13)
где m – число параллельных опытов в каждой точке симплекса; разность ∆у (между экспериментальным и теоретическим выходом)
 ; (2.14)
; (2.14)
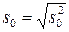 – среднеквадратичное отклонение опытных данных;
– среднеквадратичное отклонение опытных данных; 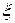 – величина, связанная с коэффициентами уравнения
– величина, связанная с коэффициентами уравнения
 , (2.15)
, (2.15)
причем
 ;
; 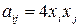 .
.
Ошибка опыта 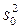 определяется также по формулам (1.138) – (1.141).
определяется также по формулам (1.138) – (1.141).
Проверка адекватности производится по неравенству
tP <fТ (l, f0, q = 0,05) (2.16)
для заданного уровня значимости; l – число коэффициентов уравнения регрессии; f0 – число степеней свободы при определении ошибки опыта.
Примечание. В некоторых исследованиях, даже если число проверочных точек g>>2, оценку адекватности уравнения регрессии проводят в каждой точке по формулам (2.13) – (2.16).
Принятие решений. Если условие (2.16) не выполняется, то уравнение регрессии признается неадекватным и его порядок повышается. Если правило композиционности выполняется, то в план включают проверочную точку и переходят к расчетам коэффициентов уравнения более высокого порядка.
Если условие (2.16) выполняется, то обычно строят изолинии (линии равного выхода) соответствующего свойства непосредственно на симплексе. Графическое изображение зависимостей свойство – состав позволяет решать задачи интерполяции и оптимизации (конечно, если число компонентов в смеси не превышает четырех).
Примечание. Если исследуемая смесевая система неоднородна, то возникают значительные трудности ее математического описания (о методах преодолевания этих трудностей см. [5]).
2.1.2. Алгоритм симплекс-решетчатых планов неполного третьего порядка для трехкомпонентной смеси.
Исходные данные. Имеется трехкомпонентная смесь. Необходимо получить зависимость некоторого свойства от состава смеси в виде (2.4) и проверить ее адекватность.
План эксперимента для рассматриваемого случая представлен в табл. 2.2 (см. рис. 2.1, б). Как и ранее, предполагается, что параллельные опыты проводятся в каждой точке симплексной решетки.
Таблица 2.2. План эксперимента
| Номер опыта | План | Выходная переменная | ||
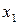
| 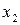
| 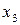
| ||
| 0,5 0,5 0,333 | 0,5 0,5 0,333 | 0,5 0,5 0,333 | 
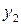
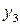
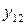



|
Расчет коэффициентов уравнения для модели (2.4) удобно проводить
β1, β2, β3 – по формуле (2.10);
β12, β13, β23 – по формуле (2.11);
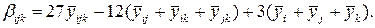 (2.17)
(2.17)
Оценка адекватности уравнения регрессии осуществляется по формулам (2.13), (2.15), (2.16), а коэффициент 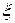 определяется по формуле
определяется по формуле
 , (2.18)
, (2.18)
где
 ;
;
 ;
;  .
.
При наличии параллельных опытов в каждой точке симплексной решетки ошибка опыта 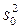 определяется по формулам (1.138) – (1.141).
определяется по формулам (1.138) – (1.141).
Принятие решений не отличается от предыдущего случая (2.1.2).
2.1.3. Алгоритм симплекс-решетчатых планов третьего порядка для трехкомпонентной смеси. Исходные данные. Имеется трехкомпонентная смесь. Необходимо получить зависимость некоторого свойства от состава смеси в виде (2.5) и проверить ее адекватность.
План эксперимента для этого случая представлен в табл. 2.3 (см. рис. 2.1, в). Предполагается, что параллельные опыты проводятся в каждой точке симплексной решетки.
Таблица 2.3. План эксперимента
| Номер опыта | План | Выходная переменная | ||
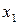
| 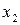
| 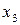
| ||
| 2/3 1/3 2/3 1/3 1/3 | 1/3 2/3 2/3 1/3 1/3 | 1/3 2/3 1/3 2/3 1/3 | 
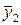
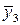
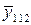




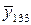

|
Коэффициенты регрессии β1, β2, β3 рассчитываются по формуле (2.10).
Коэффициенты βij рассчитываются по формулам
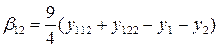 ;
;
 ;
;
 ,
,
или в общем виде
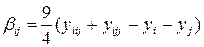 . (2.19)
. (2.19)
Коэффициенты 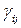 рассчитываются по формулам
рассчитываются по формулам
 ;
;
 ;
;
 ,
,
или в общем виде
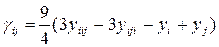 . (2.20)
. (2.20)
Коэффициенты 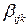 рассчитываются по формулам
рассчитываются по формулам

 ,
,
или в общем виде
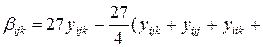
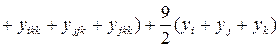 . (2.21)
. (2.21)
Оценка адекватности уравнения регрессии осуществляется по формулам (2.13), (2.14), (2.16), а коэффициент 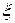 определяется по формуле
определяется по формуле
 , (2.22)
, (2.22)
где
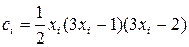 ;
;
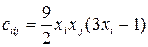 ;
;
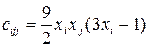 ;
;
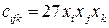 .
.
Ошибка опыта 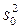 определяется также по формулам (1.138) –(1.141).
определяется также по формулам (1.138) –(1.141).
Принятие решений не отличается от предыдущих случаев (см. 2.1.2.).
Примечание. Симплексную решетку при переходе к полиномам более высоких порядков можно достраивать точками из «последующих» планов.
. Насыщенный и сверхнасыщенный планы факторного эксперимента
Введение. Одной из целей использования математической модели является грубая оценка степени воздействия факторов на выходную переменную объекта исследования. Эта цель может быть достигнута различными методами но всех их объединяет условие минимизации числа экспериментов. Этот критерий привел к построению насыщенных и сверхнасыщенных планов экспериментов, позволяющих разделить всю совокупность факторов на два класса: доминирующие факторы и «шумовой» фон (несущественные факторы).
Определение. Ненасыщенность, насыщенность и сверхнасыщенность планов определяются соотношением числа опытов плана эксперимента N и числа определенных параметров l:
N-l >0 – ненасыщенный план;
N-l = 0 – насыщенный план;
N–l < 0 – сверхнасыщенный план.
Замечание. Рассмотренные ранее планы ПФЭ и ДФЭ были ненасыщенными, а симплекс-решетчатые планы – насыщенными.
2.2.1. Алгоритм насыщенного плана дробного факторного эксперимента. Исходные данные. Имеется совокупность факторов, воздействующих на объект исследования. Известно, что степень влияния этих факторов на выходную переменную различна. Предлагается выделить существенные факторы с помощью минимально возможного числа экспериментов.
План эксперимента. Использование плана дробного факторного эксперимента в качестве насыщенного возможно при числе факторов n = 3 (N = 4), n = 7 (N = 8), n = 15 (N = 16), n = 31 (N = 32) и т.д. В этом случае можно получить математическую модель  и использовать t-критерий для отсеивания факторов.
и использовать t-критерий для отсеивания факторов.
Наличие смешанных оценок по этому плану для решения задачи отсеивания факторов не играет серьезной роли.
Расчет коэффициентов b0, b1, ..., bi, ... и оценка значимости факторов проводятся по алгоритмам 1.5.5 и 1.5.2 (в этом случае, естественно, достаточно провести параллельные опыты в одной точке).
Принятие решений. Коэффициенты, для которых tip оказалось меньше tT (1.91) (f0= N0—1, q = 0,05), относят к «шумовому» фону, остальные – считают значимыми. Иногда проверку значимости проводят по формуле, эквивалентной условию (1.91):
 (2.23)
(2.23)
где  – абсолютное значение i-го коэффициента; tT – табличное значение критерия Стьюдента;
– абсолютное значение i-го коэффициента; tT – табличное значение критерия Стьюдента;  – среднеквадратичное отклонение i-го коэффициента
– среднеквадратичное отклонение i-го коэффициента
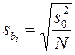 . (2.24)
. (2.24)
В этом случае коэффициенты, не удовлетворяющие условию (2.23), относятся к «шумовому» фону.
2.2.2. Алгоритм насыщенного плана Плакетта - Бермана. Исходные данные те же, что и в предыдущем алгоритме.
План эксперимента и его построение. Плакеттом и Берманом были сконструированы ортогональные насыщенные планы, число экспериментов в которых кратно четырем:
N = 4p, p = 1, 2, ... . (2.25)
Используя эти планы, можно исследовать объекты, имеющие (4р – 1) факторов. Такие планы более выгодны, чем насыщенные планы ДФЭ, поскольку удовлетворяют условиям исследования через четыре фактора.
Алгоритм построения планов следующий. Факторы изменяются на двух уровнях: +1 и – 1.
Первая строка матрицы плана задается таблицей 2.4, вторая и последующие строки получаются сдвигом всех элементов влево (или вправо) и перестановкой крайнего элемента на образовавшееся свободное место с другой стороны строки. Получаются одинаковые знаки по диагоналям матрицы. Этот процесс повторяется (N – 2) раз.
Таблица 2.4 Первые строки планов Плакетта – Бермана
| Номер опыта | Первая строка матрицы плана |
| + + + - + - - + + - + + + - - - + - + + + + - + - + + - - + - - - + + - - + + + + - + - + - - - - + + - + + + + + - + - + + - - + + - - + - + - - - - |
Последняя строка плана составляется только из элементов – 1. Матрица плана имеет размерность N×(N – 1).
Построенные таким образом планы являются ортогональными и поэтому расчет коэффициентов и оценка их значимости проводится обычными методами (см. алгоритм 1.5.2).
Замечание 1. Иногда применяется несколько иной алгоритм построения плана, дающий тот же результат. Строка табл. 2.4 используется для построения столбца плана. Следующий столбец получается сдвигом элементов первого столбца вниз или вверх и т.д. Последняя строка составляется из элементов – 1.
Замечание 2. Построение планов Плакетта-Бермана для N=28 и выше приведено в [6].
Замечание 3. Для расчета ошибки опыта 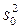 в планах Плакетта-Бермана часто используют прием фиктивных переменных. Он заключается в том, что недостающие факторы (например, если в объекте n=12, а план предусматривает n=15, то недостающих факторов n= 3) заменяются фиктивными факторами. Эффекты этих факторов отличаются от нуля, если их взаимодействия значимы и ошибки измерения отсутствуют. Если считать, что величины взаимодействия факторов малы, а
в планах Плакетта-Бермана часто используют прием фиктивных переменных. Он заключается в том, что недостающие факторы (например, если в объекте n=12, а план предусматривает n=15, то недостающих факторов n= 3) заменяются фиктивными факторами. Эффекты этих факторов отличаются от нуля, если их взаимодействия значимы и ошибки измерения отсутствуют. Если считать, что величины взаимодействия факторов малы, а  – k эффектов (коэффициентов) фиктивных переменных, то ошибка опыта будет определяться по формуле
– k эффектов (коэффициентов) фиктивных переменных, то ошибка опыта будет определяться по формуле
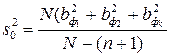 (2.26)
(2.26)
где N – число опытов по матрице планирования; п – число факторов; N – (n+1) – число фиктивных факторов.
Далее оценка проводится по (1.119), (1.131) и (2.23), (2.24). Табличное значение критерия Стьюдента находят для f=N – (n+1) степеней свободы.
Принятие решений не отличается от предыдущего алгоритма.
2.2.3. Алгоритмы метода случайного баланса (сверхнасыщенный план). Исходные данные те же, что и в предыдущих алгоритмах.
В плане эксперимента по методу случайного баланса исследуемые факторы варьируются на двух уровнях – верхнем и нижнем. Для построения матрицы планирования предлагается «чистый» случайный баланс, при котором распределение уровней в столбцах осуществляется по таблице случайных чисел, или случайное смешивание двух дробных планов ПФЭ. Один из возможных планов случайного баланса (случайное смешивание ДФЭ  и
и 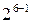 ) приведен в табл. 2.5. Условие
) приведен в табл. 2.5. Условие  должно выполняться всегда. Этот план может использоваться и для меньшего числа факторов.
должно выполняться всегда. Этот план может использоваться и для меньшего числа факторов.
Таблица 2.5. План эксперимента
| Номер опыта | План | Выходная переменная | ||||||||||||||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | y | 
| |
| - + - + - + - + - + - + - + - + | - - + + - - + + - - + + - - + + | + - - + - + + - + - -+ - + + - | + + + + - - - - - - - - + + + + | + - + + - + - - - - + + + - - + | - - - + + + + - + + - - + - -+ | + - - - + + + - - - + + - + + + | - - + - + - - + + - - - + + + + | + - + + - + + - - - + - - + + - | - + + + - + + - + - - - + + + + | + - + - + + - + + - - - + + - - | + - - + - - + - + - - - + + + + | - - + - - + + - + + - + + - + - | + + - + - + - - + + - - - - + + | y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 y14 y15 y16 | 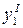
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

|
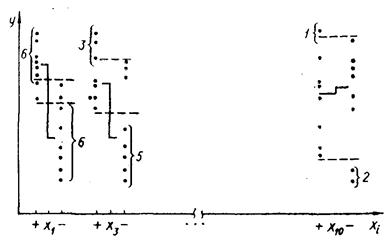
Рис. 2.2. Построение диаграмм рассеивания.
Диаграммы рассеивания строят с целью выделения факторов или их взаимодействий. Выделение осуществляют визуально. Диаграммы рассеивания строят так: по оси абсцисс откладывают значения факторов для уровней «+» и «–», а по оси ординат – значения выходной переменной (рис. 2.2.).
В каждом столбце xi диаграммы рассеивания размещены все значения выходной переменной, которые разбиваются на две группы. Одна из групп соответствует тем опытам, где фактор был на нижнем уровне, другая – где фактор был на верхнем уровне.
Среди опытных данных на каждом уровне находят медиану Ме. Медианой называется линия, по обе стороны которой находится одинаковое число точек. При нечетном числе точек медиана проходит через среднюю точку. Разность между медианами ∆Ме двух уровней характеризует качественное влияние фактора хi на выходную переменную. Таким образом, построение диаграммы рассеивания позволяет визуально по максимальному значению ∆Ме выделить наиболее значимые факторы. Для этой же цели используют так называемые выделяющиеся точки L в нижней и верхней частях диаграммы рассеивания. Для фактора х1 их число равно 6+6=12, для факторов х3 и х10 соответственно 3+5=8 и 1+2=3 и т. д. На рис. 2.2 группы выделяющихся точек отмечены фигурными скобками.
Примечание. Иногда в качестве критерия значимости факторов на диаграмме рассеивания используют произведение разности между медианами на число выделяющихся точек
 . (2.27)
. (2.27)
Последовательное выделение существенных факторов. Для количественной оценки факторов нужно отделить значимые факторы от незначимых. Процедура выделения такова. Выбирают два-три фактора, имеющие максимальную разность между медианами или максимальное число выделяющихся точек. Строят таблицу с тремя или двумя входами. Допустим, это будут факторы х1, х3, х4 (см. табл. 2.5). В клетки табл. 2.6 записывают значения выходной переменной для различных комбинаций уровней. Так, в первой клетке (слева вверху) записаны значения у4 и y14 – те значения, которые получились, когда х1, х3, х4 были на верхнем уровне и т. д.
Таблица 2.6. Подготовка данных для оценки линейных эффектов
| x4 | x3 – | х1 – | ||
| x3+ | x3 – | x3+ | x3 – | |
| «+» | 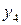
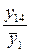
| 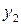

| 
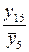
| 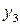
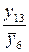
|
| «–» | 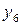
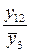
| 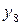

| 

| 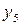
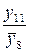
|
Вычисление линейных эффектов производят по формулам, смысл которых ясен из уравнений
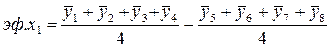 ;
;
 ; (2.28)
; (2.28)
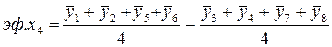 .
.
Оценки коэффициентов производят по формуле
 . (2.29)
. (2.29)
Усреднение в клетках таблицы приходится делать потому, что в случайно организованном плане эксперимента различным комбинациям уровня соответствует различное число наблюдений.
Если есть основания к изменению выходной переменной принять гипотезу нормального распределения, то значимость эффектов можно оценить по критерию Стьюдента
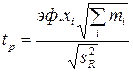 , (2.30)
, (2.30)
где mi – число наблюдений в i-ой клетке таблицы; 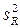 – остаточная дисперсия, находится как среднее по каждой
– остаточная дисперсия, находится как среднее по каждой  для i-ой клетки таблицы; число степеней свободы
для i-ой клетки таблицы; число степеней свободы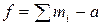 ,a – число среднеарифметических значений в таблице с несколькими входами. Оценку рассеивания
,a – число среднеарифметических значений в таблице с несколькими входами. Оценку рассеивания  для каждой клетки находят относительно средних значений
для каждой клетки находят относительно средних значений 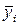 этой же клетки.
этой же клетки.
Оценка значимости эффектов по критерию Стьюдента вследствие громоздкости расчетов проводится не всегда.
Корректировка исходного вектора матрицы плана. После выделения эффектов проводят корректировку исходных данных матрицы плана. Для этого от всех уN в плане эксперимента, где факторы хi находятся на уровне «+», уменьшают на эф. xi. Получают новый вектор результатов эксперимента 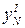 , освобожденный от влияния фактора xi. Далее строится новая диаграмма рассеивания и алгоритм повторяется.
, освобожденный от влияния фактора xi. Далее строится новая диаграмма рассеивания и алгоритм повторяется.
Таким же образом производится отсеивание эффектов парных взаимодействий.
Принятие решений. Процесс выделения существенных факторов можно закончить, если выполняется условие
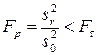
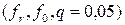 . (2.31)
. (2.31)
где  – оценка дисперсии результатов эксперимента относительно их среднеарифметического значения на r-ом шаге процедуры;
– оценка дисперсии результатов эксперимента относительно их среднеарифметического значения на r-ом шаге процедуры; 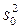 – ошибка опыта, полученная по нескольким параллельным наблюдениям.
– ошибка опыта, полученная по нескольким параллельным наблюдениям.