Подходящий закон распределения
1. На рис. 5. изображен график закона распределения для данной выборки. Этот график больше всего похож на кривую нормального закона распределения, которая имеет симметричный холмообразный вид [2, c.117].
2. Для нормального закона распределения характерны следующие равенства:
1) 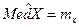
2) 
3) 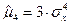
Проверим выполнение этих равенств для выборки  .
.
1) 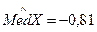 ,
, 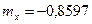 , следовательно,
, следовательно, 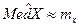
2) 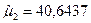 ,
, 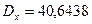 ,
, 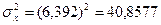 , следовательно,
, следовательно, 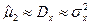
3) 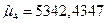 ,
, 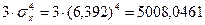 , следовательно,
, следовательно, 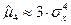
Характерные для нормального распределения равенства выполняются.
3. Для симметричного закона распределения, а нормальный закон распределения – это симметричный закон, необходимо выполнение следующих равенств: 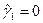 ,
, 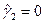 , т.е. равенство нулю несмещенных оценок коэффициента асимметрии и коэффициента эксцесса.
, т.е. равенство нулю несмещенных оценок коэффициента асимметрии и коэффициента эксцесса.
Проверим выполнение этих равенств для выборки  :
:
 , следовательно,
, следовательно, 
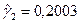 , следовательно,
, следовательно, 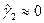
Характерные для симметричного закона распределения равенства выполняются.
4. Правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения.

Проверим выполнение этого правила для нашей выборки.
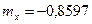
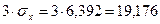
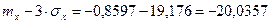
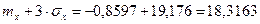
Все элементы выборки входят в отрезок  , т.е. условие, указанное в правиле трех сигм, выполняется, значит есть основание предполагать, что изучаемая величина распределена нормально.
, т.е. условие, указанное в правиле трех сигм, выполняется, значит есть основание предполагать, что изучаемая величина распределена нормально.
6.2 Критерий Пирсона 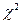
Критерий согласия - критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Существует несколько критериев согласия: 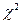 К. Пирсона, Колмогорова, критерий
К. Пирсона, Колмогорова, критерий 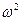 , Смирнова и т.д. Сначала рассмотрим критерий Пирсона – критерий
, Смирнова и т.д. Сначала рассмотрим критерий Пирсона – критерий 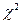 .
.
Критерий Пирсона отвечает на вопрос о том, случайно ли расхождение частот. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости е согласие или несогласие с данными наблюдений.
Прежде чем проверять гипотезу о выбранном законе распределения, сначала необходимо выдвинуть эту гипотезу (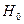 ) и конкурирующую ей (
) и конкурирующую ей (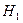 ):
):
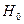 : случайная величина подчиняется нормальному закону распределения
: случайная величина подчиняется нормальному закону распределения
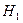 : случайная величина подчиняется другому закону распределения
: случайная величина подчиняется другому закону распределения
Для применения критерия Пирсона воспользуемся интервалами построенными ранее (таблица 4), но так как не в каждый интервал гистограммы попадает более пяти данных (интервалы 1,6,7, здесь  , см. таблицу 4), то для применения этого критерия объединим соседние столбцы гистограммы, т.е. объединяем 1,2 интервалы и 6,7 интервалы.
, см. таблицу 4), то для применения этого критерия объединим соседние столбцы гистограммы, т.е. объединяем 1,2 интервалы и 6,7 интервалы.
Для каждого интервала вычислим теоретическую вероятность попадания случайной величины в i-ый интервал гистограммы, при условии, что гипотеза 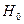 справедлива:
справедлива:  ,
,
Для каждого интервала вычислим теоретическое количество точек, попадающих в i-ый интервал: 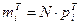 .
.
Для каждого интервала находим меру близости теоретических и практических данных i-ого интервала 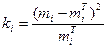
Вычислим общую меру близости:  , где r – число интервалов на гистограмме.
, где r – число интервалов на гистограмме.
Перед тем как считать теоретическую вероятность попадания случайной величины в i-ый интервал гистограммы  , необходимо нормировать случайную величину
, необходимо нормировать случайную величину 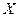 , т.е. вычислить значения
, т.е. вычислить значения  и
и 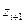 , причем наименьшее значение
, причем наименьшее значение 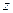 положим равным
положим равным 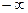 , а наибольшее -
, а наибольшее -  . Следует также напомнить значения, необходимые для вычисления
. Следует также напомнить значения, необходимые для вычисления 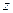 :
: 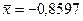 ,
, 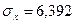 . Вычисление данных значений приводится в таблице 6.
. Вычисление данных значений приводится в таблице 6.
Результаты вычислений представлены в таблице 7.
Таблица 6
Нормирование случайной величины
| № | 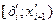
| 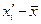
| 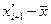
| 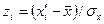
| 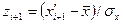
|
(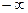 ; -6,8542) ; -6,8542)
| 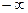
| -5,9945 | 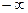
| -0,9378 | |
| [-6,8542; -2,1713) | -5,9945 | -1,3116 | -0,9378 | -0,2052 | |
| [-2,1713; 2,5116) | -1,3116 | 3,3713 | -0,2052 | 0,5274 | |
| [2,5116; 7,1945) | 3,3713 | 8,0542 | 0,5274 | 1,26 | |
[7,1945;  ) )
| 8,0542 | 
| 1,26 | 
|
Таблица 7
Результаты вычислений для критерия Пирсона
| № | 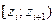
| 
| 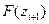
| 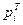
| 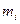
| 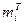
| 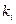
|
(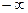 ; -0,9378) ; -0,9378)
| 0,1741 | 0,1741 | 16,5395 | 0,0176 | |||
| [-0,9378; -0,2052) | 0,1741 | 0,4189 | 0,2448 | 23,256 | 0,7789 | ||
| [-0,2052; 0,5274) | 0,4189 | 0,7009 | 0,282 | 26,79 | 3,8911 | ||
| [0,5274; 1,26) | 0,7009 | 0,8962 | 0,1953 | 18,5535 | 0,6806 | ||
[1,26;  ) )
| 0,8962 | 0,1038 | 9,861 | 0,3512 | |||
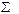
| 5,7194 |
Значит 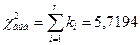
Найдем число степеней свободы распределения 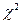 :
:  , где
, где  - количество интервалов ,
- количество интервалов , 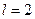 – число параметров предполагаемого закона распределения. Получим
– число параметров предполагаемого закона распределения. Получим 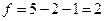
По таблице процентных точек распределения 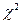 [1] находим критические значения
[1] находим критические значения 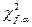 при
при 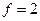 для уровней значимости
для уровней значимости  = 0,01; 0,05; 0,1:
= 0,01; 0,05; 0,1:
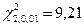
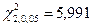
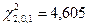
Поскольку 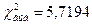 меньше критических значений
меньше критических значений 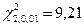 ,
, 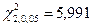 , то для уровней значимости
, то для уровней значимости  = 0,01; 0,05, согласно критерию Пирсона, нет оснований отвергнуть нулевую гипотезу. Так как
= 0,01; 0,05, согласно критерию Пирсона, нет оснований отвергнуть нулевую гипотезу. Так как 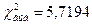 больше критического значения
больше критического значения 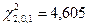 , то для уровня значимости
, то для уровня значимости  = 0,1 нулевая гипотеза отвергается.
= 0,1 нулевая гипотеза отвергается.