Лекція 18. РОЗРАХУНОК РОЗПОДІЛУ СВІТЛОВОГО ПОТОКУ ВІД РІВНОЯСКРАВОЇ ПОВЕРХНІ, ЩО СВІТИТЬ

Необхідно розрахувати освітленість і світловий потік від поверхонь кінцевих розмірів, що світять, для яких застосування закону квадратів відстані приводить до значної похибки при його використанні.

Розрахунок освітленості від поверхонь, що світять, розташовуваних звичайно в площині стелі, зводиться до визначеної освітленості від поверхні, що світить, перпендикулярної і рівнобіжної до розрахункової площини.

1.Поверхня, що світить, перпендикулярна до розрахункової площини, що відповідає завданню визначення світлового потоку, який падає зі світної стелі на одну із стін приміщення, рис 18.1.

Рис. 18.1

1. Виділимо на світній площині елемент d_1, орієнтація якого в просторі визначається нормаллю n₁;

2. Користуючись законом квадратів відстаней, неважко визначити освітленість у будь-якій точці поверхні S₂, створюваної елементом поверхні, що світить, dS₁. Виразивши силу світла елемента, що світить, dS₁ у напрямку до розрахункової точки через яскравість поверхні , одержимо

, (18.1)

де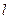– відстань від елемента, що світить, d₁ до розрахункової точки S₂;

– кут між напрямком сили світла в розрахункову точку і нормаллю до поверхні S₁;

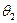– кут між напрямком сили світла в розрахункову точку

і нормаллю до поверхні S₂.

Освітленість від усієї поверхні, що світить, S₂:

. (18.2)

3. Світловий потік, що падає з поверхні, яка світить, S₁ на поверхню S₂ дозволить визначити світловий потік S₁.

Світловий потік, що падає на елемент поверхні dS₂ з поверхні S₁:

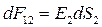. (18.3)

Повний світловий потік, що падає з поверхні S1 на поверхню S2, визначиться інтегруванням по площі поверхні S2:
. (18.4)

2. Запишемо вираз для світлового потоку, що падає з поверхні S₂ на поверхню S_1, вважаючи S₂ випромінюючою поверхнею, що і має яскравість L₂ :

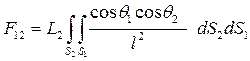. (18.5)

Порівнюючи 18.4 і 18.5, бачимо, що при рівності яскравостей L₁ і L₂ світловий потік, який падає з S₁ на S₂, дорівнює світловому потокові, що падає з поверхні S₂ на S₁ . Це теорема названа Муном теорією взаємності світлових потоків.

Ямауті використав теорему Муна для вирішення більш складних задач. Розглянемо рис.18.2.

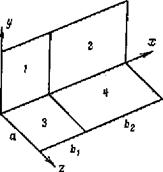
Рис. 18.2

Запишемо вираз для світлових потоків, що падають з поверхні S₁ на поверхню S₄ і з поверхні S₃ на поверхню S_{2 :}

 

; (18.6)

.

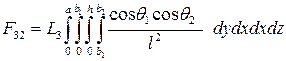Порівнюючи 18.4, 18.5 і 18.6, бачимо, що за умови рівності яскравостей L₁ =L₂ =L₃ =L₃ має місце

F14 =F41 =F32 =F23. (18.7)

У 18.4 замінимо в підінтегральному виразі і l поточними координатами x, y, z, а площі d₁ і d₂ - відповідно через dxdy і dydz. Проінтегрувавши по площах поверхонь S₁ і S₂, одержимо

(18.8)

де і .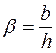

Розрахунок складний, тому з огляду на те, що тут 2 змінн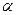і і 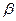, Яковлевим [21] побудовані графіки для 10, рис 18.3.

Рис. 18.3

 

По осі ординат тут F₁₂/h² для L₁=10, а по осі абсцис – відносні значення розміру сторони освітлюваного прямокутника .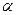

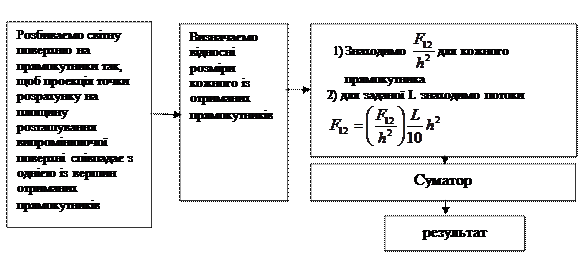
Алгоритм розрахунку світлового потоку у випадку, коли світна поверхня перпендикулярна до розрахункової площини: