Площина
Векторне рiвняння площини.Нехай в просторi вибрана
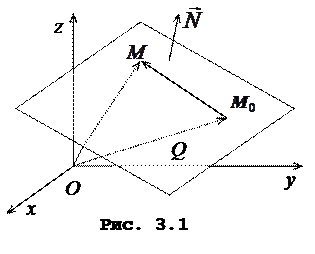 прямокутна система коорди-нат xОyz (рис. 3.1), заданi вектор
прямокутна система коорди-нат xОyz (рис. 3.1), заданi вектор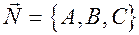 i точка
i точка 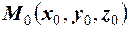 , отже, i ра-дiус-вектор цiєї точки
, отже, i ра-дiус-вектор цiєї точки
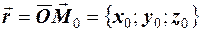 . Скла-демо рiвняння площини Q, що проходить через точку
. Скла-демо рiвняння площини Q, що проходить через точку  перпендикуляно до нор-мального вектора
перпендикуляно до нор-мального вектора  .
.
Нехай 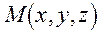 довiльна точка площини,
довiльна точка площини,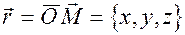
 її радiус-вектор. Побудуємо вектор
її радiус-вектор. Побудуємо вектор 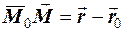 . Очевидно, що
. Очевидно, що 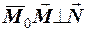 , i
, i  або
або 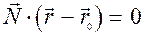 . Це i є векторне рiвняння площини Q, заданої векторами
. Це i є векторне рiвняння площини Q, заданої векторами  i
i 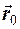 .
.
Загальне рiвняння площини. Запишемо векторне рiвняння площини в декартових координатах. Так як координати вектора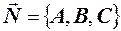 , a вектора
, a вектора 
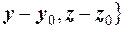 , то, виражаючи скалярний добуток через координати спiвмножникiв, одержимо:
, то, виражаючи скалярний добуток через координати спiвмножникiв, одержимо:
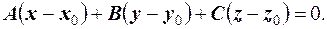 (1*)
(1*)
Це рiвняння площини, що проходить через точку 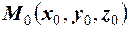 перпендикулярно до нормального вектора
перпендикулярно до нормального вектора 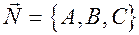 .
.
Рiвняння (1*) можна записати по-iншому:
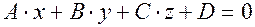 (2*)
(2*)
де 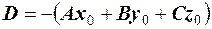 . Рiвняння (2*) називається загальним рiвнянням площини. Має мiсце таке твердження:
. Рiвняння (2*) називається загальним рiвнянням площини. Має мiсце таке твердження:
Кожне рiвняння першого степеня вiдносно x, y, z визначає в просторi площину; при цьому коефiцiєнти при x, y, z, тобто числа A, B, C є координати вектора  , нормального до площини.
, нормального до площини.