Поверхнi другого порядку

 

Множина точок 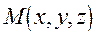простору, координати яких задовольняють алгебраїчному рiвнянню другого степеня вiдносно x, y та z називається поверхнею другого поряд-ку, що визначається цим рiвнянням.

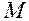Сферична поверхня. Сферичною поверхнею називають множину вciх точок простору, що знаходяться вiд за-даної точки C, що називається центром, на однiй i тiй же вiддалi R (радiус). Нехай 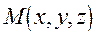- довiльна точка сфе-ричної поверхнi, центр 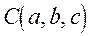, радiус R. Тодi , або

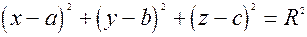
Це рiвняння сферичної поверхнi з центром в точцi 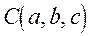радiуса R. Якщо центр сфери спiвпадає з початком координат 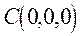, то рiвняння сферичної поверхнi

.

 

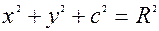Елiпсоiд. Поверхня, що визначається рiвнянням

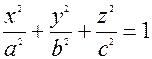, (20*)

називається елiпсоїдом. Якщо 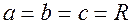, то це сферична поверхня.

Перетнемо елiпсоїд площиною . В перерiзi отримаємо лiнiю , тобто елiпс з пiввicями a i b.

В перерiзi елiпсоїда площиною xОz утворюється елiпс

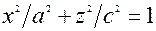
з пiввiсями a i c. В перерiзi елiпсоїда площиною yОz 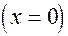одержимо елiпс

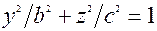з пiввicями b i c (рис. 3.16).

Якщо 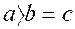, то рiвняння (20*) визначає подовжений елiпсоїд обертання з вiccю обертання Оx; якщо 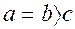, то рiвняння (20*) визначає стиснутий елiпсоїд обертання з вiссю обертання Оz. Якщо серед чисел a, b, c немає рiвних, то елiпсоiд називається трьохвiсним.

Рiвняння (20*) мiстить тiльки квадрати координат, звiдси випливає, що елiпсоїд симетричний вiдносно початку координат, а площини координат є його площини симетрiї.

Гiперболоїди. a) Однопорожнинний гiперболоїд - це поверхня, що визначається рiвнянням

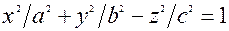, (21*)

де a,b,c - його напiввіci (рис. 3.17).

Перетинаючи поверхню (21*) площинами координат , , 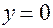, 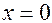одержимо в перерiзi вiдповiдно елiпс та двi гiперболи ; ; .

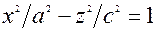В перерiзi однопорожнинного гiперболоїда площиною 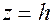, паралельною площинi xОy утворюється елiпс з пiвосями

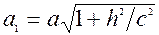та .

Однопорожнинний гiперболоїд симетричний вiдносно початку координат, а площини координат його площини симетрiї.

 

б)Двопорожнинний гiперболоїд - це поверхня, що задається рiвнянням

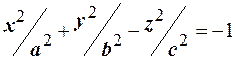, (22*)

де a, b, c - його півосі. Перетинаючи поверхню (22*) площинами , , 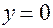, 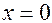одержимо в перерiзi вiдповiдно пусту множину та двi гiперболи (рис. 3.18)

, .

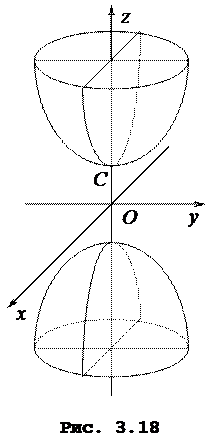
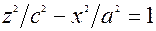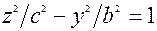В перерiзi двопорожнинного гiперболоїда площиною 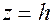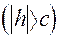утворюється елiпс з півосями

, .

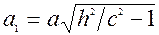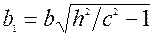Двопорожнинний гiперболоїд симетричний вiдносно початку координат; площини координат його площини симет-рiї.

Рiвняння двопорожнинного гiперболоїда обертання навколо вici Оz

.

 

Параболоїди. а) Елiптичний параболоїд - це поверхня, що визначається рiвнянням (рис. 3.19 )

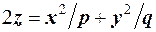(23*)

де p i q - додатнi параметри. Перетинаючи цю поверхню площинами , , 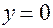, 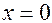одержимо в перерiзi вiдповiдно точку i двi параболи

; .

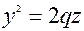Перетинаючи поверхню (23*) площиною 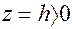, одержимо в перерiзi елiпс з пiввiсями 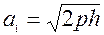i .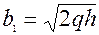

Площини xОz i yОz є площини симетрії цієї поверхні. При рівняння (23*) визначає параболоїд обертання з вісю обертання Оz

.

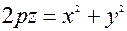б) Гiперболiчний параболоїд - це поверхня, яка описується

рiвнянням

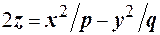(24*)

де p i q - додатнi параметри. В перетинi поверхнi (24*) площинами y=0 та x=0 утворюються параболи (рис. 3.20)

;

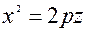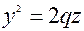
з вершинами в початку координат, симетричнi вiдносно вici Оz, з параметрами p i q.

 

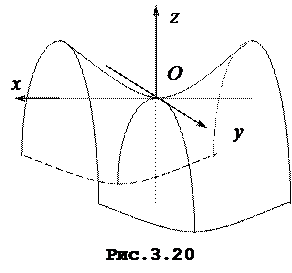Площина xОy дає в перетинi лiнiю 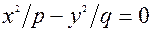, рiвняння якої розпадається на пару прямих 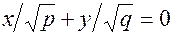, , 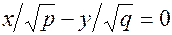що проходять через початок координат. Перетинаючи гiперболiчний параболоїд площиною z=h, одержимо в перерiзi при h>0 гiперболу

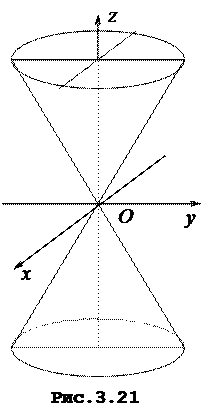
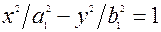, де 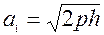, 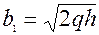його пiввіci;

а при h<0 - спряжену гiперболу

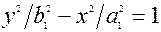, де 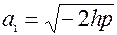, 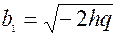пiввіci.

Так як рiвняння (24*) мicтить квадрати змiнних x та y, то площини xОz та yОz виявляються площинами симетрiї цiєї поверхнi. Гiперболiчний параболоїд має форму сiдла.

 

Конус. Конусом другого порядку називають поверхню, яка описується рiвнянням

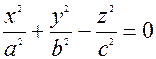(25*)

Розглянемо перетин поверхнi (25*) площиною z=0. В перерiзi одержимо точку (рис. 3.21)

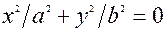Þ О(0,0)

В перерiзi площиною z=h>0 одержимо елiпс з пiввicями 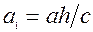та .

В перерiзi площиною xОz (y=0) одержимо лiнiю 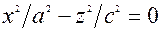, рiвняння якої розпадається на пару прямих 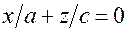, , 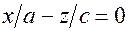що проходять через початок координат. Точка 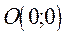- вершина конуса; елiпс

- напрямна лiнiя, а прямi та 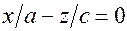- твiрнi. Якщо a=b, то конус круговий. Взагалi, конiчною називають поверхню, що утворена прямими (твiрними), що проходять через задану точку О (вершину конуса) i перетинають задану лiнiю L(напрямну).

 

Цилiндри другого порядку. Цилiндричною називають поверхню, утворену прямими (твiрними), що паралельнi де-якiй заданiй прямiй i перетинають задану лiнiю L (напрямну).

Розглянемо цилiндричнi поверхнi, твiрнi яких пара-лельнi однiй з координатних вiсей.

Рiвняння цилiндричної поверхнi, твiрнi якої пара-лельнi вici Оz, має вигляд 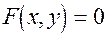. Якщо твiрнi пара-лельнi вici Оy або Оx, то рiвняння цилiндричних поверхонь мають вигляд , .

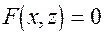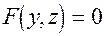Не важко помiтити, якщо в рiвняннi поверхнi вiдсутня одна змiнна x чи y або z, то це рiвняння цилiндричної поверхнi з твiрними, паралельними тiй віcі, змiнна якої вiдсутня.

 

 

 

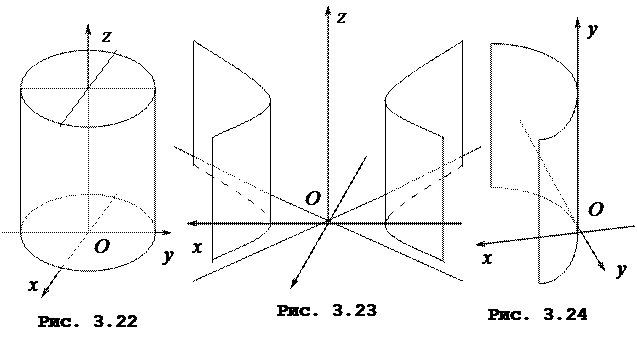
Якщо напрямна цилiндричної поверхнi - лiнiя другого порядку, то поверхня називається цилiндром другого по-рядку. На рис. 3.22 зображений елiптичний цилiндр

.

На рис. 3.23 та на рис. 3.24 показанi гiперболiчний та параболiчний цилiндри

; .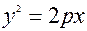