ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ
Рассмотрим плоский изгиб стержня, загруженного сосредоточенной силой Р (рис. 1.2).
На некотором расстоянии z выделим сечение (точка А), у которого будет некоторый прогиб y и угол поворота q. На расстоянии dz от прежнего сечения выделим еще одно сечение (точка В) прогиб которого y+dy, а угол поворота q-dq. Эти два сечения образуют между собой угол dq, пересекаясь в некоторой точке О. Расстояние АО=ВО=r, где r - радиус кривизны балки.
Длина дуги dS, образованная этими двумя сечениями может быть найдена как:
 . .
|

Рис.1.2.
Из элементарного треугольника (рис. 1.2), приняв АВ»dS, получим
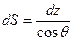 , ,
 или или 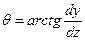 . .
|
Кривизна балки определится как
 . .
|
Продифференцируем угол поворота по координате
 . .
|
Используем известную тригонометрическую зависимость
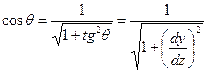 . .
|
Объединяя полученные зависимости, получим кривизну балки в виде:
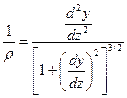 . .
| (1.1) |
Известно, что кривизна балки связана с внутренними силовыми факторами соотношением:

|
Приравнивая правые части уравнений, получим полное дифференциальное уравнение изогнутой оси балки:
 . .
| (1.2) |
Зачастую в инженерных расчетах угол поворота является небольшой величиной и составляет q <1…20. При таких углах
 , тогда , тогда
| |
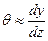 , ,
| (1.3) |
т.е. в первом приближении можно полагать, что угол поворота является первой производной от прогиба (1.1) по координате. Также проанализируем знаменатель правой части уравнения.
При 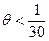 рад, получим
рад, получим
 . .
|
Очевидно, что погрешность такого допущения не превышает 0,1%, поэтому в инженерной практике часто используют приближенное уравнение изогнутой оси бруса:
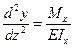 . .
| (1.4) |
Очевидно, что уравнение является дифференциальным 2-го порядка. Интегрируя это уравнение при известной функции моментов Мx(z), можно получить функцию углов поворота и прогибов сечений балки:
 , ,
| (1.5) |
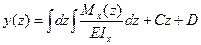 . .
| (1.6) |
Константы интегрирования С и D определяются в зависимости от граничных условий балки – условий закрепления балки на опорах.
| Пример 1.1. Вычислить прогиб и угол поворота на консоли длиной L при действии сосредоточенной силы P (рис. 1.3). Введем правостороннюю систему координат, совместив ее начало с левым краем балки. Выделим некоторое сечение с координатой z. Изгибающий момент в этом сечении определится как: |  Рис.1.3.
Рис.1.3.
|
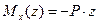 . .
|
Используем уравнение, получим
 . Интегрируя по координате обе части получим . Интегрируя по координате обе части получим
| |
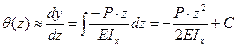 . .
|
Константу С найдем из условия жесткого закрепления балки на опоре, т.е.  . Получим
. Получим
 , откуда , откуда 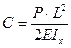 . Тогда функция углов поворота примет вид: . Тогда функция углов поворота примет вид:
| |
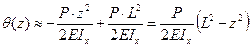 . .
| (1.7) |
Интегрируя по координате еще раз, получим уравнение прогибов
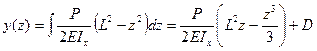 . .
|
Константу D найдем из условия жесткого закрепления балки на опоре, т.е.  .
.
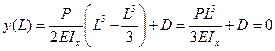 , откуда
, откуда  .
.
Тогда функция прогибов примет вид:
 . .
| (1.8) |
По условию необходимо знать прогиб и угол поворота на консоли, т.е. при z=0. Подставим z=0 в уравнения (1.7) и (1.8), получим
 , ,
 . .
|
Угол поворота сечения на консоли имеет знак «+», следовательно, поворот сечения происходит против часовой стрелки. Прогиб этого сечения имеет знак «-», что означает перемещение сечения вниз.
При наличии на балке большего количества участков решение задачи усложняется, поскольку на каждом из участков уравнение моментов имеет различный вид. В этих случаях на практике используются специальные методы вычисления перемещений, например, метод начальных параметров, метод Верещагина и др. Изучение этих методов вычисления перемещений выходит за рамки настоящего курса.