Дискретні випадкові величини

Випадкова величина X називається дискретною, якщо: 1) сукупність її можливих значень можна перерахувати – x₁, x₂,..., x_n (або x₁, x₂,..., x_n,...); 2) можна знайти відповідні ймовірності p_k = P{X = x_k} того, що випадкова величина X приймає ці значення.

Набір ймовірностей p_k називають розподілом випадкової величини X. Розподіл містить вичерпну інформацію про випадкову величину. Якщо у проміжок [c; d) попадають лише значення x_i, x_i+1,..., x_j випадкової величини X, то подія XÎ[c; d) є сумою попарно несумісних подій X= x_i, X= x_i+1,…, X=x_j. Тому на підставі формули (1) розділу 1.2 одержимо:

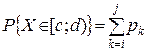. (3)

Із формули (3) виходять такі наслідки:

1) 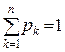– умова нормування;

2) F_X (x) = å p_k, де знак суми стосується лише тих значень k, для яких x_k < x. Звідси випливає, що значення функції розподілу дискретної випадкової величини у проміжку (x_k; x_k+1] дорівнює p₁+p₂+...+p_k. Приблизний графік функції розподілу дискретної випадкової величини зображено на мал.2.2.

Відзначимо слідуючий факт: будь-яка сукупність чисел p_k ³ 0, таких, що å p_k = 1, визначає розподіл деякої випадкової величини.

Приклад 1. Дискретна випадкова величина X задається таблицею розподілу

X	-1
P	0.3	0.1	a	0.35

Знайти: 1) a; 2) F_X (x); 3) P{X > – 0.3}; 4) P{X≤ 1.7}.

Розв‘язок. 1) Значення a знаходиться із умови нормування:

0.3+0.1+a+0.35=1 Þ a=0.25.

2) Функцію розподілу знаходимо на основі наслідку 2, а її графік приведено на мал.2.3.

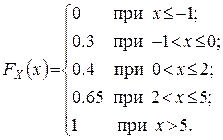
3) P{X > – 0.3} = P{X = 0} + P{X = 2} + P{X = 5} = 0.7.

4) P{X≤ 1.7} = P{X = 0} + P{X = – 1} = 0.4.

Розглянемо кілька найбільш важливих дискретних розподілів.

1) Біноміальний розподіл (розподіл Я. Бернуллі). Випадкова величина X приймає значення 0,1,...,n і при цьому

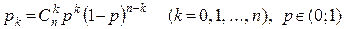. (4)

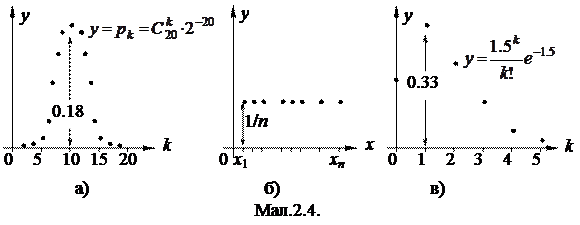Біноміальний розподіл має випадкова величина, що дорівнює кількості появ події A у серії з n незалежних випробувань при ймовірності p її появи в одному експерименті. На малюнку 2.4.а) наведено графік біноміального розподілу при n=20, p=0.5.

2) Геометричний розподіл. Випадкова величина X приймає значення 0,1,... і при цьому p_k = p(1– p) ^k–1 (k =1,2,...). Геометричний розподіл має випадкова величина, що дорівнює кількості повторень випробувань до першої появи події A при ймовірності p її появи в одному експерименті.

3) Рівномірний дискретний розподіл. Випадкова величина X приймає n значень з відповідними ймовірностями, що дорівнюють 1/n (мал.2.4.б).

4) Розподіл Пуассона. Випадкова величина X приймає значення 0,1,... з ймовірностями

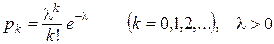. (5)

На малюнку 2.4.в) наведено графік розподілу Пуассона з параметром l=1.5. На підставі формули (2) розділу 1.5 кількість рідкісних подій має розподіл Пуассона.