Перетворення розподілів

Нехай розподіл випадкової величини X є відомим. Потрібно знайти розподіл випадкової величини Y, яка пов’язана з функціональною залежністю Y=g(X) (Y приймає значення g(x), коли X приймає значення x).

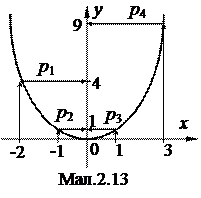1) Випадкова величина X є дискретною. Тоді знаходять сукупність значень випадкової величини Y і ймовірності, з якими ці значення приймаються. У тому випадку, коли серед значень g(x_k) немає однакових, маємо P{Y=g(x_k)}=P{X=x_k}=p_k . Якщо серед значень g(x_k) є однакові, потрібно додавати відповідні ймовірності.

Приклад 1. Випадкова величина X задана таблицею розподілу:

Знайти таблицю розподілу випадкової величини Y=X².

Розв‘язок. Метод побудови таблиці розподілу випадкової величини зрозумілий з мал.2.13: вона має вигляд

 

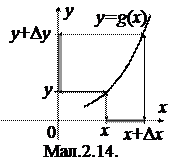2) Випадкова величина X є неперервною. У тому випадку, коли функція g(x) має обернену h(y), справедливе співвідношення

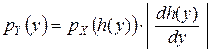, (11)

яке виходить з того, що події {XÎ[x; x+Dx)} та {YÎ[y; y+Dy)} є еквівалентними (мал.2.14).

Зауваження. Якщо функція не є монотонною, то формулу (11) слід використати на кожному проміжку монотонності а потім об’єднати одержані результати.

Приклад 2. Випадкова величина X~N(a;s²). Знайти щільність ймовірності випадкової величини: 1) Y=AX+B; 2) Y=e^X.

Розв’язок. 1) Оскільки y=Ax+B, то і . Тому на підставі (11), одержимо

.

Таким чином, Y~N(aA+B; s²A²).

2) Оскільки оберненою по відношенню до функції e^x ( g(x) ) є функція ln y( h(y) ), то і на підставі формули (11) одержимо

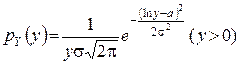. (12)

Розподіл (12) називається логнормальним. Він використовується при опису амплітуди, потужності та обвідної радіосигналу. Графік логнормального розподілу приведено на мал.2.15.

Приклад 3. Випадкова величина X~N(a;s²). Знайти щільність ймовірності випадкової величини Y=X².

Розв’язок. Функція y=x² має дві обернені h₁(y) =, h₂(y) = –. Тоді, за формулою (11) з урахуванням зауваження знаходимо

.

Графік цього розподілу при s=1 приведено на мал.2.16.