Неперервний випадковий вектор

Випадковий вектор називається неперервним, якщо його координати X та Y є неперервними випадковими величинами (іншими словами, ймовірність попадання у будь-яку наперед фіксовану точку дорівнює нулю). У цьому випадку існує невід’ємна функція – щільність ймо­вір­ності випадкового вектора – така, що ймовірність попадання випадкового вектора у довільний малий прямокутник П{[x₀; x₀+Δx), [y₀; y₀+Δy)} (мал.2.17) має вигляд

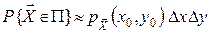. (3)

Співвідношення (3) дозволяє довести, що ймовірність попадання вектора в будь-яку область площини D знаходиться за формулою

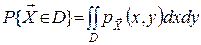. (4)

Із співвідношення (4) випливають такі наслідки:

1) 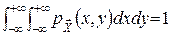(умова нормування, яка означає, що об’єм тіла, обмеженого поверхнею та площиною , дорівнює одиниці);

2) .

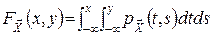Оскільки 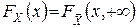і , то із наслідку 2 знаходимо вираз для щільностей ймовірності координат через щільність ймовірності вектора (умови узгодженості)

(5)

Відновити щільність ймовірності випадкового вектора за щільностями ймовірності його координат можна не завжди.

Умовна щільність ймовірності p_X (x /Y=y) випадкової величини X при умові Y=y визначається співвідношенням

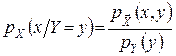. (6)

Останнє співвідношення можна записати у вигляді, подібному до теореми множення ймовірностей

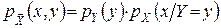. (6')

Випадкова величина X називається незалежною від випадкової величини Y, якщо при всіх значеннях x,y виконується рівність p_X (x / Y=y)=p_X (x). Із (6) виходить, що поняття незалежності є взаємним. Випадкові величини X та Y незалежні тоді і тільки тоді, коли справедливе співвідношення

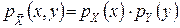. (7)

Якщо випадкові величини X та Y не є незалежними, то вони називаються залежними. Ця залежність може бути або функціональною – Y=g(X), або мати імовірнісний (стохастичний) характер, коли значення, яке приймає одна величина лише впливає на закон розподілу іншої.

У іншому випадку мова може йти лише про наближене представлення випадкової величини Y функцією випадкової величини X:

Y»g(X).

При цьому функція g(X) вибирається так, щоб звести до мінімуму (в якомусь сенсі) похибку цієї наближеної рівності.

Приклад 1. Випадковий вектор 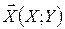розподілений в області D{(x;y): 0<x<1, x<y<1} з щільністю ймовірності . Знайти: 1) ко­ефіцієнт A; 2) щільності ймовірності координат; 3) умовні щільності ймовірності; 4) ймовірність попадання в область D₁{(x;y): 0<x<1/2, x<y<1–x}.

Розв’язок. 1) Виходячи з умови нормування одержуємо (мал.2.18.а)

;

2) Із умов узгодженості (5) одержуємо

, якщо xÎ[0;1],

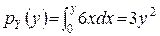, якщо yÎ[0;1].

3) На підставі формули (6) та результатів пункту 2 знаходимо:

, якщо 0<x<y, yÎ(0;1),

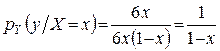, якщо x<y<1, xÎ(0;1).

Випадкові величини X та Y є залежними.

4) 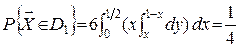(мал.2.18.б).

Проінтегрувавши рівність (6') по змінній y та скориставшись умовою узгодженості (5), знайдемо аналог формули повної ймовірності

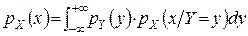. (8)