Найважливіші види двовимірних розподілів.
1) Рівномірний розподіл. Випадковий вектор називається рівномірно розподіленим у області D, якщо
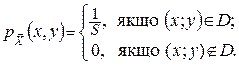
S - площа області D.
 Якщо двовимірний вектор
Якщо двовимірний вектор  рівномірно розподілений у прямокутнику зі сторонами, паралельними осям координат, то координати X та Y будуть незалежними рівномірно розподіленими випадковими величинами. Наведемо приклад залежних величин, які самі і у сукупності розподілені рівномірно.
рівномірно розподілений у прямокутнику зі сторонами, паралельними осям координат, то координати X та Y будуть незалежними рівномірно розподіленими випадковими величинами. Наведемо приклад залежних величин, які самі і у сукупності розподілені рівномірно.
Приклад 1. Нехай випадковий вектор 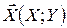 рівномірно розподілений в області D=D1ÈD2 (мал. 2.19). Знайти щільності ймовірності координат вектора.
рівномірно розподілений в області D=D1ÈD2 (мал. 2.19). Знайти щільності ймовірності координат вектора.
Розв’язок. Сума площ фігур D1 і D2 дорівнює 1/2 (половина площі квадрата із стороною 1) і тому

На підставі умов узгодженості (формула (5) розділ 2.2), маємо

Таким чином, випадкова величина X рівномірно розподілена на відрізку [0;1]. Аналогічно доводиться, що випадкова величина Y також рівномірно розподілена на відрізку [0;1]. Оскільки  ¹pX(x)×pY(y), то випадкові величини X та Y будуть залежними.
¹pX(x)×pY(y), то випадкові величини X та Y будуть залежними.
 Приклад 2. Випадкові величини X та Y незалежні і розподілені рівномірно у проміжку [0;1]. Знайти ймовірність того, що корені квадратного рівняння Xx2+x+Y=0 дійсні.
Приклад 2. Випадкові величини X та Y незалежні і розподілені рівномірно у проміжку [0;1]. Знайти ймовірність того, що корені квадратного рівняння Xx2+x+Y=0 дійсні.
Розв’язок. Невід’ємність дискримінанта рівносильна умові X·Y . Вектор
. Вектор 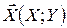 рівномірно розподілений у квадраті D{(x; y): 0£ x£1, 0£ y£1} і тому
рівномірно розподілений у квадраті D{(x; y): 0£ x£1, 0£ y£1} і тому  Таким чином,
Таким чином,

 .
.
Область інтегрування D1 розташована у квадраті D вище гіперболи xy=1/4 (див.мал.2.20).
2) Двовимірний нормальний розподіл. Випадковий вектор називається розподіленим за нормальним законом (законом Гауса) з параметрами a1, a2, s12, s22, r, якщо його щільність розподілу має вигляд:
 , (9)
, (9)
де | r |<1, s1>0, s2>0.
При r=0 із (9) одержуємо двовимірний закон Гауса в найпростішій формі
 . (10)
. (10)
Функція  , визначена рівністю (9), набуває максимального значення у точці (a1;a2), яка називається центром розсіювання, і постійне значення на еліпсах
, визначена рівністю (9), набуває максимального значення у точці (a1;a2), яка називається центром розсіювання, і постійне значення на еліпсах
 .
.
 Ці еліпси, що називаються еліпсами рівної ймовірності або еліпсами розсіювання, дають уявлення про форму поверхні
Ці еліпси, що називаються еліпсами рівної ймовірності або еліпсами розсіювання, дають уявлення про форму поверхні  . При r=0 і s1=s2 еліпси перетворюються в кола, а при | r |»1 стають «витягнутими» і «тонкими». Більша вісь еліпса повернута на кут
. При r=0 і s1=s2 еліпси перетворюються в кола, а при | r |»1 стають «витягнутими» і «тонкими». Більша вісь еліпса повернута на кут  відносно осі Ox (мал.2.21).
відносно осі Ox (мал.2.21).
З розподілу (9) виходить, що випадкові величини X та Y розподілені за законами Гауса X~N(a1;s12) та Y~N(a2;s22). Проте, добуток цих законів дає не розподіл (9), а (10). Тому координати двовимірного випадкового вектора, розподіленого за законом Гауса у найпростішій формі, є незалежними випадковими величинами, а за законом Гауса у загальній формі – залежними. Умовні щільності ймовірності також є Гаусовими. Наприклад, умовна ймовірність


співпадає з  .
.
Ймовірність попадання випадкового вектора в область ефективно може бути знайдена тоді, коли r = 0 і область D є прямокутником з сторонами, паралельними осям координат, або коли D ‑ область, обмежена еліпсом розсіювання.
 Приклад 3. Гармата обстрілює злітно-посадочну смугу шириною 60м та довжиною 200м. Координати точки попадання снаряда по відношенню до системи координат, осі якої направлені вздовж та поперек смуги, а початок знаходиться у її центрі (мал.2.22), розподілені за законом
Приклад 3. Гармата обстрілює злітно-посадочну смугу шириною 60м та довжиною 200м. Координати точки попадання снаряда по відношенню до системи координат, осі якої направлені вздовж та поперек смуги, а початок знаходиться у її центрі (мал.2.22), розподілені за законом
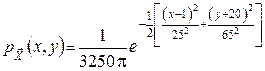 .
.
Знайти ймовірність попадання у смугу при одному пострілі.
Розв’язок.  (Випадкові величини X та Y незалежні). Оскільки X~N(1м; 252 м2), Y~N(–20м; 652 м2), то на підставі формули (10) розділу 2.1 одержуємо
(Випадкові величини X та Y незалежні). Оскільки X~N(1м; 252 м2), Y~N(–20м; 652 м2), то на підставі формули (10) розділу 2.1 одержуємо
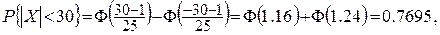
 .
.
Отже, ймовірність попадання у смугу дорівнює 0.66.
3) Розподіл Релея. Нехай випадковий вектор 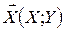 розподілений за законом Гауса у найпростішій формі (10) з параметрами a1=a2=0, s12=s22=s2.
розподілений за законом Гауса у найпростішій формі (10) з параметрами a1=a2=0, s12=s22=s2.
Тоді випадкова величина  – відстань від точки (X;Y) до початку координат – розподілена за законом Релея з параметром s2 (графік щільності приведено на мал.2.23):
– відстань від точки (X;Y) до початку координат – розподілена за законом Релея з параметром s2 (графік щільності приведено на мал.2.23):
 . (11)
. (11)
 Розподіл Релея виникає у такій важливій задачі. Розглянемо гармонічні коливання з періодом T :
Розподіл Релея виникає у такій важливій задачі. Розглянемо гармонічні коливання з періодом T :
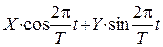 .
.
Як відомо з курсу елементарної математики (фізики), такі коливання можна зобразити у вигляді
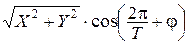 .
.
Нехай X та Y незалежні випадкові величини, розподілені за законом Гауса N(0;s2). Тоді виявляється, що амплітуда  та початкова фаза коливань j будуть незалежними випадковими величинами. При цьому амплітуда буде мати релеєвський розподіл з параметром s2, а початкова фаза буде рівномірно розподілена у проміжку [0;2p).
та початкова фаза коливань j будуть незалежними випадковими величинами. При цьому амплітуда буде мати релеєвський розподіл з параметром s2, а початкова фаза буде рівномірно розподілена у проміжку [0;2p).
У тому випадку, коли випадковий вектор  розподілений за законом Гауса у найпростішій формі (10) з параметрами a1, a2, s12=s22=s2, випадкова величина
розподілений за законом Гауса у найпростішій формі (10) з параметрами a1, a2, s12=s22=s2, випадкова величина 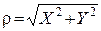 виявляється розподіленою за законом Райса
виявляється розподіленою за законом Райса
 ,
,
де I0(x) = . При великих значеннях
. При великих значеннях  закон Райса є близьким до нормального
закон Райса є близьким до нормального 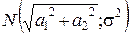 .
.
4) Розподіли c2 (Пірсона), t (Стьюдента) та Fn,m (Фішера). Ці розподіли будуть використовуватися у главі 5.
Нехай випадкові величини X0, X1,X2,..., Xn є незалежні та розподілені за законом Гауса N(0;1). Розподіл випадкової величини cn2=X12+X22+...+Xn2 називається c2‑розподілом (хі-квадрат розподілом) з n степенями свободи. Щільність ймовірності випадкової величини cn2 задається співвідношенням (графік щільності приведено на мал.2.24)
 ,
,
де стала Kn визначається умовою нормування. Зокрема, випадкова величина c12 = X12 має щільність ймовірності
 .
.
Цей результат уже приводився в прикладі 3 пункту 2.1.4.
Розподіл випадкової величини  називається t‑розподілом (розподілом Стьюдента) з n степенями свободи. Щільність ймовірності випадкової величини tn задається співвідношенням (графік щільності приведено на мал.2.25):
називається t‑розподілом (розподілом Стьюдента) з n степенями свободи. Щільність ймовірності випадкової величини tn задається співвідношенням (графік щільності приведено на мал.2.25):
 |
 ,
,
де стала Ln визначається умовою нормування.
Графік щільності є симетричним відносно прямої x=0 і подібний до графіка щільності нормального розподілу N(0;1). Із зростанням кількості ступенів свободи n розподіл Стьюдента наближається до нормального з параметрами a=0, s2=1. В таблиці 2 додатка приведені значення te(n), які задовольняють рівності
 .
.
 Ці значення більші, ніж значення de, що є коренями рівняння 2Ф(de)=1–e. Але із зростанням кількості ступенів свободи te(n) наближається до de. Наприклад, для e=0.05 маємо t0.05(5)=2.5706, t0.05(10)=2.2281, t0.05(20)=2.0960, t0.05(+¥)=d0.05=1.963 (мал.2.26).
Ці значення більші, ніж значення de, що є коренями рівняння 2Ф(de)=1–e. Але із зростанням кількості ступенів свободи te(n) наближається до de. Наприклад, для e=0.05 маємо t0.05(5)=2.5706, t0.05(10)=2.2281, t0.05(20)=2.0960, t0.05(+¥)=d0.05=1.963 (мал.2.26).
Розглянемо випадкову величину  , де
, де  і
і 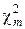 – незалежні випадкові величини, розподілені за законом χ2 відповідно з n та m ступенями свободи. Розподіл випадкової величини Fn,m називається розподілом Фішера з n та m ступенями свободи. Щільність цього розподілу має вигляд
– незалежні випадкові величини, розподілені за законом χ2 відповідно з n та m ступенями свободи. Розподіл випадкової величини Fn,m називається розподілом Фішера з n та m ступенями свободи. Щільність цього розподілу має вигляд
 ,
,
де стала A знаходиться із умови нормування.