Закон розподілу суми випадкових величин

Теорема. Нехай випадкові величини X та Y незалежні та мають щільності ймовірностей p_X(x) і p_Y(y). Тоді щільність ймовірності випадкової величини Z=X+Y є згорткою щільностей ймовірності доданків

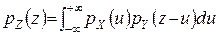. (12)

Наслідки. 1) Якщо випадкові величини X_i незалежні і X_i ~N(a_i;s_i²), то X₁+...+X_n ~N(a₁+...+a_n; s₁²+...+s_n² ).

2) Якщо випадкові величини X_i незалежні і розподілені за показниковим законом з параметром l, то їх сума h=X₁+...+X_n розподілена за законом Ерланга n–1-го порядку з параметром l

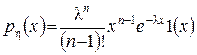. (13)

3) Сума двох незалежних випадкових величин, розподілених за законом Пуассона з параметрами l₁ і l₂, розподілена за законом Пуассона з параметром l₁+l₂.

Виняткова роль розподілу Гауса може бути пояснена таким чином: якими б не були закони розподілу незалежних доданків, закон розподілу суми буде близьким до гаусевого, якщо вклади кожного з доданків у суму приблизно одинакові і число доданків достатньо велике. Так, наприклад, помилка вимірювання породжується спільною дією великого числа причин; розподіл цих помилок добре узгоджується з законом Гауса.

Точне формулювання приведеного вище твердження складає зміст знаменитої центральної граничної теореми, у розробці якої одну з головних ролей зіграв видатний математик професор Харківського університету академік О.М.Ляпунов. Виявилось, що основну умову цієї теореми – припущення про незалежність доданків – можна суттєво послабити. Цей напрямок бере початок від іншого видатного математика професора Харківського університету академіка С.Н.Бернштейна. Йому належить також і перша за часом аксіоматика теорії ймовірностей (1917р).

Приклад 1. Літак розраховано на чотирьох пасажирів або вантаж вагою не більше 360 кг. Припустимо, що вага пасажирів є випадковою величиною, розподіленою за законом Гауса N(75 кг; 256 кг²). Як часто літак буде перевантаженим, якщо на борт береться чотири пасажири.

Розв’язок. Позначимо через X_i (i=1,...,4) вагу i-го пасажира. Оскільки випадкові величини X_i незалежні, то на підставі наслідку 1) одержимо

X= X₁+X₂+X₃+X₄ ~N(300 кг; 1024 кг²).

Застосуємо формулу (10) розділу 2.1:

.

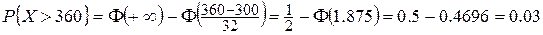Таким чином, тільки в трьох рейсах із ста очікується перевантаження літака.