Математичне сподівання випадкової величини
Означення 1. Математичним сподіванням випадкової величини X називається число MX, яке в залежності від типу випадкової величини визначається формулою
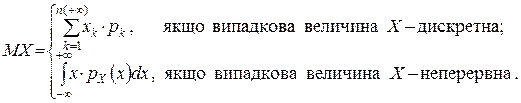(1)
Математичне сподівання дає уяву про розташування значень випадкової величини.
Розмірність математичного сподівання MX співпадає з розмірністю випадкової величини X.
Приклад 1. Нехай подія A з’являється у випробуванні з імовірністю p. Знайти математичне сподівання числа появ події A в даному випробуванні.
Розв’язок. Позначимо число появ події A у випробуванні через X. Величина X – випадкова, приймає свої значення 0 і 1 з імовірностями 1– p та p. Тоді на підставі формули (1) (верхній рядок) одержимо
MX=0·(1– p)+1·p.
Приклад 2. Знайти математичне сподівання випадкової величини X, розподіленої по закону Пуассона з параметром l (розділ 2.1, формула (5)).
Розв’язок. Оскільки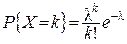 
(k=0,1,...) , то згідно з формулою (1) маємо
.
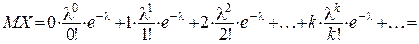
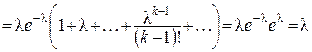Приклад 3. Знайти математичне сподівання випадкової величини X, розподіленої за показниковим законом з параметром l (розділ 2.1, формула (8)).
Розв’язок. На підставі формули (1) (нижній рядок) одержимо
.
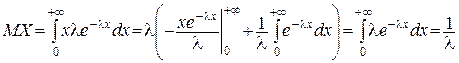Звідси виходить, що середній проміжок часу T між двома послідовними відмовами апаратури дорівнює 1/l, якщо тривалість проміжку часу між двома послідовними відмовами апаратури розподілена за показниковим законом з параметром l. З цієї причини показниковий розподіл у теорії надійності записується у вигляді
,
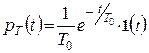де T0 ‑ середній час роботи до відмови.
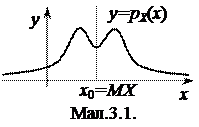При обчисленні математичного сподівання доцільно використовувати такий результат.
Теорема 1. Якщо розподіл випадкової величини X симетричний відносно прямої x=x0, то MX=x0 (мал.3.1).
Наслідки: 1) Математичне сподівання випадкової величини, розподіленої по закону Гауса N(a; s2), дорівнює a.
2) Математичне сподівання рівномірного у проміжку [c; d] розподілу дорівнює (c+d)/2.
3) Математичне сподівання випадкової величини, розподіленої за законом Стьюдента tn, дорівнює 0.
Приклад 4. Знайти математичне сподівання випадкової величини, розподіленої за законом Релея з параметром s2 (розділ 2.2, формула (11)).
Розв’язок. За формулою (1) маємо
.
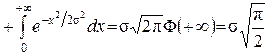