Кореляційний момент випадкових величин

Означення 1. Кореляційним моментом (кореляцією, коваріацією) K(X,Y) випадкових величин X та Y називається число

K(X,Y)=M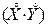. (10)

Ця величина має розмірність, що дорівнює добутку розмірностей випадкових величин X та Y. Скориставшись властивостями математичного сподівання, можна привести формулу (10) до вигляду

K(X,Y)=M(X·Y)–MX·MY. (11)

Випадкові величини називаються корельованими при K(X,Y)¹0 і некорельованими при K(X,Y)=0. Якщо випадкові величини незалежні, то із (9) виходить, що K(X,Y)=0 – із незалежності випадкових величин випливає їх некорельованість. Якщо K(X,Y)¹0, то випадкові величини є залежними ‑ із корельованості випадкових величин випливає їх залежність. Однак, із K(X,Y)=0 не випливає незалежність випадкових величин – із некорельованості випадкових величин не випливає їх незалежність. Приклад таких величин приведено в зауваженні до теореми 3 пункту 3.1.4. Отже,

Незалежність Þ некорельованість

Корельованість Þ залежність

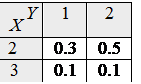Приклад 1. Знайти кореляційний момент координат випадкового вектора, заданого таблицею:

Розв’язок. За формулами (5) та (7) знаходимо

Тоді за формулою (11) одержимо

K(X,Y)=3.5–2.2·1.6= – 0.02.

Приклад 2. Випадковий вектор рівномірно розподілений в області D{(x;y): 0<y<x², 0<x<1} (мал.3.2). Знайти коре­ляційний момент його координат.

Розв’язок. Площа області D дорівнює 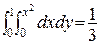. Отже, 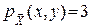, якщо (x; y)ÎD. Тому на підставі формул (5), (7), (11) маємо: