Дисперсія випадкової величини та її властивості

Після того, як математичне сподівання випадкової величини знайдено, виникає питання, наскільки сильно значення випадкової величини від­хиляється від математичного сподівання. Характеристикою ступеня розсіювання випадкової величини навколо математичного сподівання є математичне сподівання квадрата флуктуації випадкової величини (математичне сподівання флуктуації не придатне, тому що воно завжди дорівнює нулю). Інколи в якості характеристики розсіювання випадкової величини використовують математичне сподівання абсолютної величини її флуктуації.

Означення 1. Дисперсією випадкової величини називається невід’ємне число

DX=M()². (1)

Розмірність дисперсії дорівнює квадрату розмірності випадкової величини. Тому вводять також величину , що називається середнім квадратичним (стандартним) відхиленням, вимірність якої співпадає з вимірністю випадкової величини.

Чим менше s_X (DX), тим тісніше групуються значення випадкової величини навколо її математичного сподівання.

Дисперсія допускає важливе математичне тлумачення. Нехай i – сила струму, що проходить через резистор з опором 1 Ом. Тоді потужність, яка виділяється флуктуаційною складовою струму дорівнює 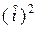, а її середнє значення M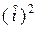. Таким чином, дисперсія струму дорівнює середній потужності, яка виділяється флуктуаційною складовою струму на резисторі з одиничним опором.

При знаходженні дисперсії, як правило, використовують не формулу (1), а інший вираз, який одержується з правої частини цієї формули на підставі властивостей математичного сподівання:

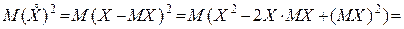
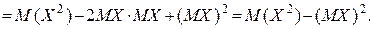
Таким чином,

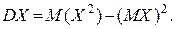(2)

Якщо X=Y , то кореляційний момент дорівнює дисперсії K(X,X)=DX. Запишемо формулу (2) у розгорнутому вигляді

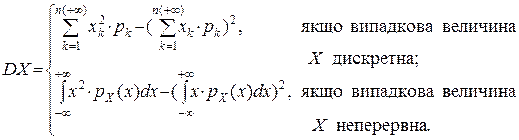(2´)

Із формули (1) випливає, при сталих k і l, важлива властивість дисперсії

D(kX+l)=k²DX. (3)

Дійсно, з урахуванням властивостей математичного сподівання, одержимо

D(kX+l)=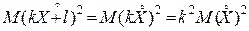=k ²·DX.

Зокрема, дисперсія константи (сталої величини) дорівнює нулю.

Приклад 1. При умові прикладу 1 пункту 3.1.2 знайти дисперсію випадкової величини X.

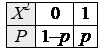Розв’язок. Із прикладу 1 пункту 3.1.2 маємо MX=p. Оскільки то MX ²=0·(1–p)+1·p=p і на підставі формули (2) одержимо

DX=p– p²=p·(1– p).

Приклад 2. Знайти дисперсію випадкової величини X, розподіленої за законом Пуассона (розділ 2.1, формула (5)).

Розв’язок.

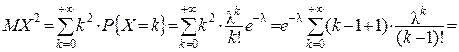
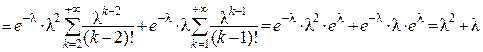
(тут двічі використане розкладання експоненти у ряд 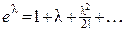). Було показано (приклад 2 пункту 3.1.2), що MX=l . Отже, DX=l²+l–l²=l – параметр закону Пуассона співпадає як з математичним сподіванням, так і з дисперсією.

Приклад 3. Знайти дисперсію випадкової величини X, розподіленої: 1) рівномірно в проміжку [c; d]; 2) за показниковим законом з параметром l; 3) за законом Гауса з параметрами a і s²; 4) за законом Релея з параметром s².

Розв’язок. При розв’язанні будуть використані формули (2) та (1) і також результати пункту 3.1.2 (приклади 3,4, наслідки теореми 1).

1) ;

2)

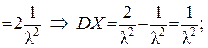
3)

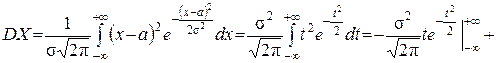
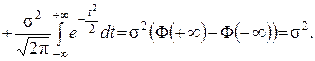
Таким чином, параметрами закону Гауса N(a;s²) є математичне сподівання a і дисперсія s²;

4)

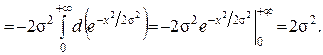
Отже, .

Випадкова величина X називається нормованою, якщо MX=0, DX=1. Прикладом нормованої випадкової величини є випадкова величина 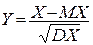. Дійсно,

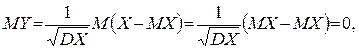
Приклад 4. Знайти математичне сподівання і дисперсію випадкової величини c_n² (c²‑розподілом з n степенями свободи).

Розв’язок. c_n²=X₁²+X₂²+...+X_n², де X_i - незалежні та розподілені за законом Гауса N(0;1). Використовуючи властивості математичного сподівання та дисперсії, одержимо:

Mc_n²=M(X₁²)+...+M(X_n²)=nM(X_i²), Dc_n²=D(X₁²)+...+D(X_n²)=nD(X_i²).

Оскільки DX_i=M(X_i²)–(MX_i)², то M(X_i²)=DX_i+(MX_i)²=1,

D(X_i²)=M(X_i⁴)–(M(X_i²))²=M(X_i⁴)–1. Отже Mc_n²=n. Залишилось знайти величину

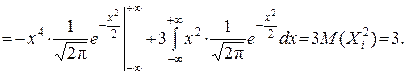
Тому =3–1=2 і остаточно Dc_n²=2n.

Зауваження. Для знаходження математичного сподівання і дисперсії нелінійної функції f(X) часто користуються наближеними формулами:

Mf(X) » f(MX),

Df(X) » | f ´(MX)|² ·DX.

Ці формули тим точніші, чим менше f(X) функція відрізняється від лінійної. Для лінійної функції f(X)=kX+l наведені формули є точними.