Дисперсія суми випадкових величин
Теорема. 1) Якщо випадкові величини X та Y корельовані (отже, залежні), то
D(X+Y)=DX+DY+2K(X,Y); (4)
2) Якщо випадкові величини X та Y незалежні (отже, некорельовані), то
D(X+Y)=DX+DY. (5)
Доведення.
1) D(X+Y )=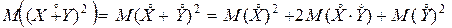 
=
=DX+DY+2K(X,Y);
2) незалежність Þ K(X,Y)=0.
Рівність (5) має місце для будь-якого скінченого числа незалежних (отже, попарно некорельованих) випадкових величин:
D(X1+X2+...+Xn)=DX1+DX2+...+DXn. (5´)
Зокрема, якщо всі випадкові величини Xi мають однаковий розподіл і незалежні, то D(X1+X2+...+Xn)=nDX1 і внаслідок цього
.
Останній результат означає, що при великій кількості незалежних вимірювань (випробувань) середнє арифметичне результатів спостереження буде близьким до вимірюваної величини.
Приклад 1. Нехай випадкові величини X1,...,Xn незалежні і однаково розподілені (зокрема, MXi=a, DXi=s2 (i=1,..., n)). Знайти математичне сподівання і дисперсію випадкової величини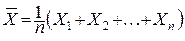 
.
Розв’язок. Використовуючи властивості математичного сподівання (формули (3) і (6) розділу 3.1) і дисперсії (формули (3) і (5)) одержимо
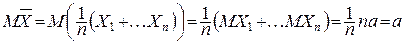
(тут незалежність випадкових величин не грає ніякої ролі),
.
Таким чином, відхилення випадкової величини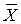 
від математичного сподівання a із зростанням n спадає, при цьому її значення 
=(x1+x2+…+xn) ⁄n (середнє арифметичне результатів спостережень) приблизно дорівнює a.
Приклад 2. Знайти дисперсію випадкової величини X - кількості появ події A у серії з n незалежних випробувань.
Розв’язок. Застосуємо метод, використаний при розв’язанні прикладу 1 пункту 3.1.4, використаємо (5‘) і результат прикладу 1 пункту 3.2.1. Оскільки X=X1+X2+...+Xn, де незалежні випадкові величини Xi приймають значення 0,1 з імовірностями відповідно 1–p, p, то DX=DX1+DX2+...+DXn= =nDX1= np(1–p). Звідси випливає, що дисперсія частоти X/n появ події A така
.
Приклад 3. В умовах прикладу 2 пункту 3.1.4 знайти дисперсію випадкової величини h.
Розв’язок. На підставі (5‘) і результату прикладу 3 пункту 3.2.1 Dη=n ∕ λ2.
Приклад 4. В умовах прикладу 1 знайти математичне сподівання випадкової величини 
.
Розв’язок. Перетворимо суму до зручного для обчислень вигляду:
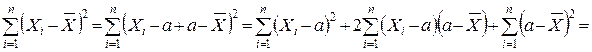
Тому
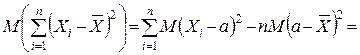
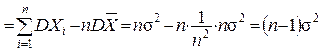
і, таким чином,
.
Можна показати, що D(S 2) із зростанням n прямує до нуля. З урахуванням одержаного вище результату, це означає, що числа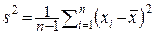 
, які є значеннями випадкової величини S 2 у конкретних серіях вимірювань, групуються навколо числа s2.
Приклад 5. Нарівні з середнім квадратичним відхиленням мірою розсіювання випадкової величини є також середнє відхилення d - математичне сподівання модуля флуктуації:
.
Знайти середнє відхилення випадкової величини X~N(a;s2).
Розв’язок.
