Нерівність П.Чебишева

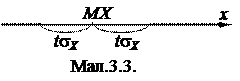Нерівність П.Чебишева встановлює верхню межу для ймовірності відхилення випадкової величини від її математичного сподівання. А саме (мал.3.3),

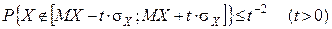. (6)

Ця оцінка ймовірності не залежить від закону розподілу випадкової величини X. Із (6) видно, що чим менше DX, тим менш ймовірні великі відхилення ts_X значень випадкової величини від математичного сподівання.

Поклавши в (6) t=3, одержимо

.

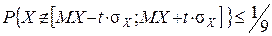Нерівність Чебишева, як правило, завищує ймовірності великих відхилень. Наприклад, для закону Гауса

P{XÏ[a–3s; a+3s]}=1–P{XÎ[a–3s; a+3s]}=1– Ф(3)=0.0027.

Однак, можна навести приклади розподілів, для яких вона дає точну величину ймовірності відхилення (наприклад, P{X=-1}=P{X=1}=1/18, P{X=0}=8/9, t=3).

Приклад 1. Оцінити з допомогою нерівності Чебишева ймовірність відхилення частоти появи події A в серії з n випробувань Я.Бернуллі від ймовірності p появи події в одному випробуванні.

Розв’язок. Математичне сподівання і дисперсія чистоти X/n появи події були знайдені відповідно у прикладах 1 пункту 3.1.4 та 2 пункту 3.2.2: M(X/n)=p, D(X/n)=p(1– p)/n. Отже, на підставі нерівності (6) одержуємо

.

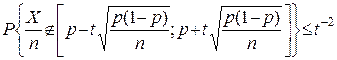Оскільки p(1–p)£1/4, то з попередньої нерівності виходить грубіша оцінка

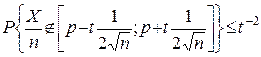. (7)

При достатньо великому t>0 права частина останньої нерівності як завгодно мала. Таким чином, довільно малою є ймовірність відхилення частоти події A від ймовірності p на величину більшу за 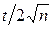. Вибираючи n достатньо великим, це відхилення можна зробити як завгодно малим. Інакше кажучи, при достатньо великому n значне відхилення частоти від ймовірності є практично неможливим. Це виправдовує підхід до визначення ймовірності p як деякого числа, навколо якого групуються частоти (див. пункт 1.2.1).

Нерівність (7) можна використати для розв’язку задачі перевірки гіпотези (докладно ця задача обговорюється у розділі 5.4).

Перевірка гіпотези. Нехай ймовірність p появи події A в одному випробуванні невідома, а кількість появ події A у даній серії з n випробувань Я.Бернуллі дорівнює k. Висунемо гіпотезу (припущення), що невідома ймовірність дорівнює p₀. Наскільки добре ця гіпотеза узгоджена з результатами експерименту? В основу розв’язку цієї задачі покладено такий принцип: якщо у даному випробуванні відбувається подія, яка при зробленому припущенні є практично неможливою, то це припущення суперечить результатам експерименту.

Вибираємо мале число e >0 (рівень значущості) і вважаємо практично неможливими події, ймовірність яких менша e. Із (7) виходить, що для практично неможливої події і допустиме відхилення значення частоти від ймовірності дорівнює . Якщо одержане в експерименті відхилення | k/n–p₀| перевищує допустиме, то висунута гіпотеза суперечить результатам експерименту.