Коефіцієнт кореляції та кореляційна матриця

Означення 1. Коефіцієнтом кореляції r_X,Y випадкових величин X та Y називається число

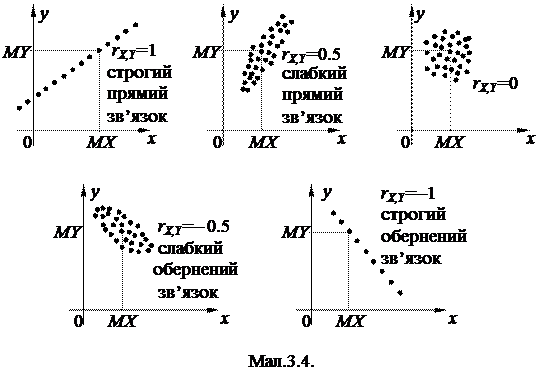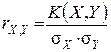. (1)

Коефіцієнт кореляції є безвимірною величиною. Абсолютна величина коефіцієнта кореляції змінюється від нуля (X та Y некорельовані, але можуть бути зв’язаними функціональною залежністю, відмінною від лінійної) до одиниці (X та Y зв’язані лінійно – Y=kX+l): 0£ |r_X,Y | £ 1. Якщо r_X,Y >0 (додатна кореляція, прямий зв’язок), то X і Y мають тенденцію зростати і спадати одночасно. Наприклад, додатна кореляція існує між продуктивністю праці та заробітною платою, між зростом людини та її вагою. Якщо r_X,Y < 0 (від’ємна кореляція, обернений зв’язок), то при зростанні однієї випадкової величини інша має тенденцію спадати і навпаки. Наприклад, від’ємна кореляція спостерігається між продуктивністю праці та вартістю одиниці продукції, між об’ємом продукції та затратами на один виріб.

Наведемо типові діаграми зв’язку між величинами X та Y при різних значеннях r_X,Y (мал.3.4).

Коефіцієнт кореляції є лише мірою лінійної залежності. Чим ближчий коефіцієнт кореляції по модулю до одиниці, тим сильніше залежність X і Y нагадує лінійну і навпаки.

Мірою залежності коефіцієнт кореляції є тільки тоді, коли випадковий вектор 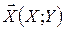розподілений за законом Гауса (формула (9) розділу 2.2). У цьому випадку можна показати, що r_X,Y=r. Тоді рівність r_X,Y =0 означає r=0. Але при r=0 закон (9) розділу 2.2 переходить у закон (10) розділу 2.2, що відповідає незалежності X і Y.

Закон Гауса: некорельованість Û незалежність

Означення 2. Кореляційною матрицею (матрицею коваріації) випадкового вектора 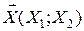називається симетрична матриця K другого порядку, елементами якої є K_ij=K(X_i,X_j):

. (2)

Можна показати, що вектор математичного сподівання і кореляційна матриця для закону Гауса (формула (9) розділу 2.2) мають вигляд:

.

Введемо у розгляд вектор 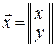. Тоді закон Гауса (9) можна записати у стислому вигляді:

, (3)

де T – операція транспонування, K^–1 – матриця, обернена до K, detK - визначник матриці K.

Форма запису (3) справедлива і для n-вимірних нормальних розподілів 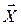(X₁; X₂; …; X_n). У цьому випадку

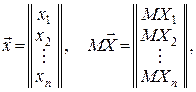
матриця K є симетричною матрицею n-го порядку

.

Крім того, число (2p)² під радикалом у формулі (3) потрібно замінити на (2p)ⁿ.

Приклад 1. В умовах прикладу 1 пункту 3.1.5 знайти коефіцієнт кореляції і кореляційну матрицю випадкових величин X і Y.

Розв’язок. Знайдемо дисперсію X і Y:

.

Використавши формули (1) та (2), одержимо:

.

Приклад 2. Випадкові величини X₁, X₂, X₃, X₄, X₅ - попарно некорельовані і мають однакові дисперсії s². Знайти коефіцієнти кореляції випадкових величин: 1) Y₁=X₁+X₂; Y ₂=X₃+X₄+X₅; 2) Y ₃=X₁+X₂+X₃; Y ₄=X₁+X₃+X₅.

Розв’язок.

1)

;

2)

.

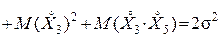Внаслідок формули (5) розділу 3.2 одержимо DY₃=DY₄=3s². Отже, на підставі формули (1) 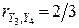.