Регресія

Якщо ми знаємо розподіл однієї координати випадкового вектора при умові, що інша координата приймає певне значення, то можна ввести поняття умовного математичного сподівання.

Означення 1. Умовним математичним сподіванням M(Y/X=x) випадкової величини Y при умові, що випадкова величина X=x, називається число, яке знаходиться за формулою

(4)

Аналогічно визначається умовне математичне сподівання M(X/Y=y).

При зміні x, взагалі кажучи, змінюється умовне математичне сподівання M(Y/X=x), яке можна розглядати у цьому випадку як функцію x:

M(Y/X=x)=g(x).

Ця функція називається регресією Y на X (Y відносно X), а її графік y=g(x) – лінією регресії Y на X.

Аналогічно визначається регресія X на Y і лінія регресії X на Y:

M(X/Y=y)=h(y), x=h(y).

Випадкові величини X та Y називаються лінійно корельованими, якщо лінії регресії є прямими. Рівняння цих прямих такі:

(5)

Зміст регресії Y на X полягає у тому, що функція g(X) є найкращим наближенням до випадкової величини Y. Це означає, що для довільної функції v(X) виконується співвідношення:

M[Y–v(X)]² ³ M[Y–g(X)]².

Якщо лінія регресії Y на X (X на Y) не є прямою, можна використати першу (другу) із прямих регресії (5) в якості наближення до істинної лінії регресії. У цьому випадку ця пряма називається прямою наближеної регресії. У зв’язку з цим відзначимо, що функція (функція 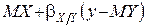) є найкращим наближенням до Y (до X) серед усіх лінійних функцій випадкової величини X (випадкової величини Y).

Зауважимо, що координати випадкового вектора, розподіленого за законом Гауса (формула (9) розділу 2.2), лінійно корельовані.

Кутові коефіцієнти b_Y/X і b_X/Y прямих регресії (5) називаються відповідно коефіцієнтами регресії Y на X та X на Y. При цьому

(6)

Прямі регресії (5) проходять через точку з координатами (MX; MY). При |r_X,Y |=1 прямі регресії співпадають, а при r_X,Y=0 – паралельні осям координат.

У якості міри розсіювання випадкової величини Y відносно регресії g(X) (Y на X) розглядають кореляційне відношення

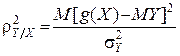. (7)

Із (7) випливають такі властивості кореляційного відношення:

1) ;

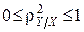2) 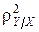=1 тоді і тільки тоді, коли між випадковими величинами X та Y є функціональна залежність Y=g(X);

3) 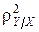=0 тоді і тільки тоді, коли g(X)=MY, тобто лінія регресії є горизонтальною прямою і, таким чином, випадкові величини X та Y є некорельованими.

Взагалі кажучи, .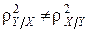

Приклад 1. В умовах прикладу 1 пункту 2.2.3 знайти лінії регресії Y на X та X на Y.

Розв’язок. На підставі (4) (нижній рядок) одержимо:

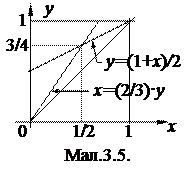
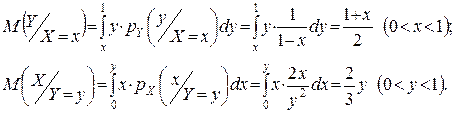
Таким чином, лініями регресії є прямі y=(1+x)/2 (Y на X) і x=(2/3)·y (X на Y) (мал.3.5).

Приклад 2. Випадковий вектор 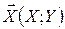має такі числові характеристики: MX=1, DX=4, MY=2, DY=9, r_X,Y=0.8. У даному випробуванні випадкова величина мала значення X=1.3. Яке математичне сподівання випадкової величини Y ?

Розв’язок. Скористаємося рівнянням прямої наближеної регресії Y на X (5):

.

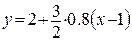Підставляючи в це рівняння x=1.3, одержимо y=2.36. Таким чином, M(Y/X=1.3)»2.36.