Теорія масового обслуговування.
Ця теорія є одним з найважливіших розділів прикладної теорії ймовірності. Теорія масового обслуговування вивчає функціонування систем, у які поступають виклики (вимоги) на обслуговування. Моменти надходження викликів, а також тривалість проміжку обслуговування кожного виклику є випадковими величинами. З такими системами зустрічаємося скрізь: телефонна і автозаправна станції, квиткова каса, злітно-посадочна смуга, перукарня і т.п.
Нехай у момент надходження чергового виклику всі обслуговуючі пристрої системи зайняті. В залежності від того, як організована схема обслуговування, системи масового обслуговування (СМО) розподіляються на такі категорії:
1) системи зі втратами – виклик одержує відмову (не обслуговується, губиться) і залишає систему (АТС);
2) системи з очікуванням – виклик ставиться в чергу і очікує на обслуговування (станція швидкої медичної допомоги). Відзначимо, що не завжди виклики обслуговуються у порядку надходження до системи. Наприклад, деякі відмови ЕОМ повинні виявлятись і усуватись відразу;
3) системи з очікуванням при обмеженні довжини черги (часу чекання).
Теорія масового обслуговування дозволяє за відомими законами розподілу кількості викликів, що надходять, і тривалості їх обслуговування одержати ймовірнісні характеристики організованості системи обслуговування: ймовірність відмови, середній час очікування початку обслуговування, математичне сподівання довжини черги, математичне сподівання часу простою і т.п.
Позначимо через N(t) кількість викликів на обслуговування, що поступили до системи за проміжок часу тривалістю t. Як правило, припускають, що виконується умова
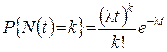(k=0,1, 2,...),
де параметр l, який називається інтенсивністю потоку викликів, дорівнює математичному сподіванню кількості викликів, що поступили до системи за одиницю часу. (Розподіл величини N(t) є розподіл Пуассона з параметром lt).
Тривалості обслуговування різних викликів вважаються взаємно незалежними випадковими величинами, які розподілені за показниковим законом з параметром m. Оскільки математичне сподівання тривалості обслуговування дорівнює 1/m, то інтенсивність потоку обслужених викликів (кількість за одиницю часу) за умови неперервної роботи дорівнює m.
n–канальна система з втратами (n телефонних ліній).
Така система в кожен момент часу може знаходитись в одному з n+1 станів: E0 (всі канали вільні), E1 (зайнятий один канал),..., En (зайняті всі канали).
 |
Орієнтований граф переходів із одного стану до іншого та відповідні інтенсивності переходів показані на мал.3.6. Перехід із стану Ek у стан Ek+1 (зліва направо) (k=0, 1,..., n–1) відбувається за рахунок потоку викликів на обслуговування інтенсивністю l. Перехід із стану Ek+1 у стан Ek (справа наліво) (k=1, 2,..., n) відбувається за рахунок потоку обслужених викликів, інтенсивність якого дорівнює (k+1)m. Наприклад, для переходу E2®E1 байдуже, який з двох зайнятих каналів звільниться. Тому інтенсивність потоку обслужених викликів буде дорівнювати сумі інтенсивностей потоків обслужених цими каналами викликів m+m=2m (приклад 2 пункту 3.1.4).
Нехай X(t) – кількість каналів, зайнятих у момент часу t (t³0) і pk(t)=P{ X(t)=k} – ймовірність перебування системи у стані Ek (k=0,1,...,n). Враховуючи припущення про характер потоку викликів і часу їх обслуговування, можна показати, що у системі встановиться стаціонарний режим:
,
причому
,
де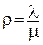 
.
Ймовірність відмови, тобто ймовірність того, що у момент надходження виклику всі n каналів зайняті, дорівнює pn.
Знайдемо математичне очікування кількості зайнятих каналів у стаціонарному режимі:
.
Приклад 1. Розглядається чотириканальна система зі втратами. Параметри вхідного потоку викликів і показникового часу обслуговування дорівнюють відповідно l=3 вик/с і m=0.75 вик/с. Знайти ймовірності відмови і математичне сподівання кількості зайнятих каналів.
Розв’язок. Оскільки r=l/m=4, то ймовірність p4 чергового виклику одержати відмову (всі канали зайняті) дорівнює
.
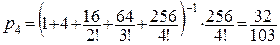Математичне сподівання кількості зайнятих каналів дорівнює 4·(1‑32/103)=2.76. Таким чином, приблизно третина каналів простоює, хоча майже 30% викликів не обслуговується. Ця типова ситуація викликана хаотичним характером надходження вимог на обслуговування і тим, що тривалість проміжку обслуговування виклику є випадковою величиною. Якби ці причини були відсутніми, відмов не було б: за одиницю часу поступає 3 заявки на обслуговування і обслуговується 3=4·3/4 заявки.
 |
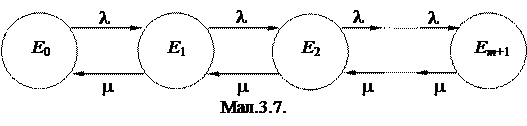Одноканальна система з чергою довжиною m з обслуговуванням у порядку надходження (АЗС з однією колонкою і площадкою, що вміщує не більше m машин).
Система може знаходитись в одному з m+2 станів: E0 – канал обслуговування вільний, E1 – канал зайнятий, E2 – канал зайнятий і один виклик стоїть у черзі,..., Em+1 - канал зайнятий і у черзі стоять m викликів (мал.3.7).
Нехай X(t) – кількість викликів, що знаходяться у системі в момент часу t (t³0) і pk(t)=P{X(t)=k} – ймовірність перебування системи у стані Ek (k=0,1,...,m+1). Можна показати, що у системі з часом виникає сталий режим:
,
причому
pk=rk(1– r)/(1– rm+2) (k=0, 1,..., m+1),
де .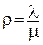
Математичні сподівання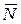 
кількості викликів у черзі (середня довжина черги) і 
часу чекання до початку обслуговування (середній час перебування в черзі) відповідно дорівнюють
 |
n–канальна система з очікуванням (обслуговування в порядку надходження викликів). Система може знаходитись в одному з нескінченої кількості станів Ek (k=0, 1, 2,...), де стан Ek означає, що в системі знаходиться k викликів. Стани Ek (k=0, 1, 2,..., n) відповідають відсутності черги. У станах Ek (k=n, n+1,...) є черга довжиною k–n. Схема переходів з одного стану в інший приводиться на мал.3.8.
Нехай X(t) – кількість викликів, що знаходяться у системі в момент часу t (t³0) і pk(t)=P{X(t)=k} – ймовірність перебування системи у стані Ek (k=0,1,2,...). Можна довести, що усталений режим можливий лише при r=l/nm<1 («швидкість» обслуговування більша за «швидкість» надходження викликів). При цьому
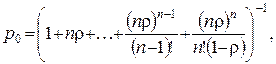
Ймовірність П=pn+pn+1+... того, що виклик на обслуговування попадає в чергу, дорівнює
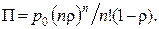
Математичні сподівання кількості викликів у черзі 
і часу чекання до початку обслуговування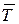 
відповідно дорівнюють
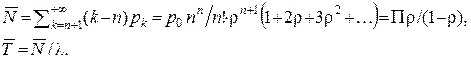
Зокрема, для одноканальної системи одержимо формули:
.
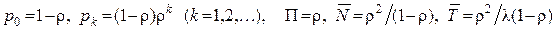Приклад 2. Бензозаправочна станція має п’ять бензоколонок, у кожній з яких на заправку автомобіля витрачається в середньому 8 хвилин. Знайти середню довжину черги і середній час перебування в черзі, якщо потік автомобілів, що прибувають на заправку, має інтенсивність λ=0.5 авт/хвил.
Розв’язок. Маємо СМО з очікуванням, у якої n=5, 1/m=8 хвил/авт, r=l/nm=4/5. Ймовірність p0 того, що система вільна дорівнює
.
Ймовірність П того, що прибулий автомобіль попаде у чергу дорівнює
.
Середня довжина черги дорівнює
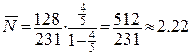авт.
Середній час очікування у черзі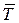 
дорівнює
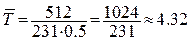хвил.
Приклад 3. Довідкове бюро обслуговує одна телефоністка, в якої два телефони. Якщо підчас відповіді по одному телефону дзвонить інший, то вона, піднявши трубку, пропонує абоненту почекати і обслуговує його після того, як покладе трубку першого телефона. Інтенсивність потоку викликів λ=2 викл/хвил, середня тривалість відповіді 1/m=3/2 хвил/викл. Знайти середній час очікування відповіді і середню довжину черги.
Розв’язок. Маємо одноканальну СМО з чергою довжиною m=1, r=l/m=3. Середня довжина черги дорівнює
викл.
Середній час очікування відповіді 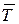дорівнює
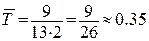хвил.