Найпростіші задачі теорії надійності

Головне питання теорії надійності полягає в визначенні ймовірнісних характеристик працездатності системи, якщо відома її структура і ймовірносні характеристики працездатності окремих елементів.

Нехай випадкова величина T – час роботи системи (або окремого її вузла) до моменту втрати працездатності (до відмови). Важливою характеристикою працездатності є математичне сподівання часу безвідмовної роботи MT.

Приклад 1. Показати, що MT=, де P(t) – функція надійності (пункт 2.1.3, зауваження).

Розв’язок. Нехай p_T (t) – щільність ймовірності випадкової величини T. Тоді p_T (t)=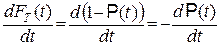. Використавши формулу інтегрування по частинах, одержимо

.

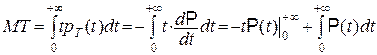Оскільки P(+¥)=0, то .

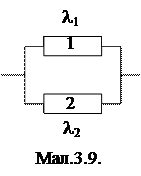
Приклад 2. Час безвідмовної роботи кожного із двох незалежних паралельно з’єднаних елементів (навантажений резерв) розподілений за показниковим законом з параметрами l₁ і l₂ відповідно. Знайти середній час безвідмовної роботи блока (мал. 3.9).

Розв’язок. Із теорем додавання і множення ймовірностей випливає, що

P(t)=P₁(t)+P₂(t) –P₁(t)·P₂(t),

де P(t), P₁(t), P₂(t) – відповідно функції надійності блока, першого і другого елемента. Оскільки P₁(t)=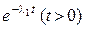, P₂(t)=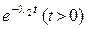(пункт 2.1.3, зауваження), то

P(t)= .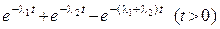

Таким чином, середній час безвідмовної роботи блоку на підставі результату прикладу 1 дорівнює

.

Якщо l₁=l₂=l, то MT=3/(2l), що у півтора рази перевищує час безвідмовної роботи одного елемента.

Приклад 3. Система складається із двох паралельно з’єднаних незалежних елементів. Час безвідмовної роботи кожного розподілений за показниковим законом з параметрами l₁ і l₂ відповідно. До моменту виходу із ладу елемента 1 елемент 2 вимкнено. Він включається в роботу в момент виходу із ладу елемента 1 (ненавантажений резерв). Знайти функцію надійності системи і середній час роботи блоку до відмови.

Розв’язок. Нехай T₁ і T₂ відповідно час безвідмовної роботи першого і другого елементів, T – час безвідмовної роботи системи (мал.3.10). Тоді T=T₁+T₂ і, таким чином, на підставі результату прикладу 1 маємо

(тут P₁(t), P₂(t) – функції надійності першого і другого елементів відповідно). Функцію надійності системи P(t) знайдемо таким чином:

P(t)=1-F_T(t)=1–P{T<t}=1–P{T₁+T₂< t}.

Оскільки щільності ймовірностей незалежних випадкових величин T₁ і T₂ відомі, то щільність ймовірності їх суми T=T₁+T₂ можна знайти за формулою (12) розділу 2.2. При цьому потрібно замінити границі інтегрування:

–∞ на 0 внаслідок додатності T₁, а +∞ на z внаслідок додатності T₂:

.

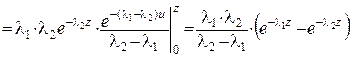Тепер знайдемо ймовірність P{T₁+T₂< t}:

P{T₁+T₂< t}=P{T< t}=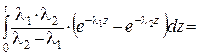

==

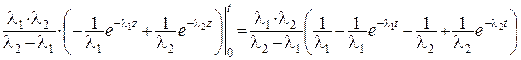=1–.

І, нарешті, P(t)=1– (1–)=.

Якщо l₁=l₂=l, то на підставі формули (13) розділу 2.2 p_T (t)=λ²t·e^-λt·1(t), і, таким чином,

P(t)=

.

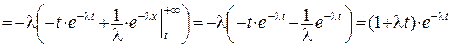При цьому MT=.