Формула повної ймовірності
Часто для вивчення випробування, з яким пов’язана подія A, корисно ввести до розгляду події Hk, для яких із тих чи інших міркувань відомі ймовірності P(Hk), P(A/Hk).
Теорема. Нехай події Hk (k=1,...,n) складають повну систему. Тоді для будь-якої події A справедлива рівність
P(A) = P(H1)·P(A/H1) + ... + P(Hn)·P(A/Hn). (5)
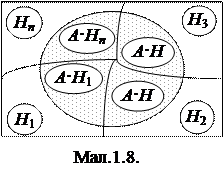
Доведення. Оскільки W=H1ÈH2È...ÈHn, то подію A можна представити у вигляді суми попарно несумісних подій A = A·H1ÈA·H2È...ÈA·Hn (мал.1.8).
Послідовно застосовуючи теореми додавання та множення ймовірностей (формули (1) розділу 1.2 та формули (2) розділу 1.3), одержимо:
.
Якщо P(Hi)=0, то відповідна складова у сумі повинна бути опущена.
Інколи формулою повної ймовірності називають співвідношення
P(A) = åP(A·Hi).
Приклад 1. По каналу зв’язку можуть передаватись з ймовірностями, рівними p0 та p1 =1 – p0, два сигнали – "0" та "1". Внаслідок дії перешкод можливі викривлення сигналів: "0" переходить в "1" з імовірністю p0,1, а "1" в "0" з імовірністю p1,0 (мал.1.9). Яка ймовірність одержати на приймальному кінці каналу сигнал "0"?
Розв’язок. Розглянемо припущення: H0 – послано сигнал "0", H1 – послано "1". Нехай подія A – це одержання сигналу "0". Тоді P(A/H0)=1 – p0,1, P(A/H1)=p1,0, P(H0)=p0, P(H1)=1 – p0. З формули повної ймовірності (9) маємо: P(A) = p0 (1 – p0,1) + (1 – p0) p1,0.
Приклад 2. Система складається з п’яти незалежних елементів, з’єднаних так, як показано на мал.1.10.а). Знайти надійність (ймовірність безвідмовної роботи) системи, якщо надійність k-го елемента дорівнює pk.
 |
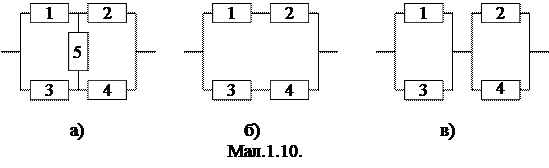Розв’язок. Нехай подія A означає, що система працює безвідмовно. Розглянемо такі припущення: H1 – п’ятий елемент працює безвідмовно, H2 – п’ятий елемент виходить з ладу. Надійність системи при умові безвідмовної роботи п’ятого елемента – P(A/H1) – співпадає з надійністю системи, зображеної на мал.1.10.в). Отже, на основі результату прикладу 2.б) пункту 1.3.1, одержимо:
P(A/H1) = (p1+p3 – p1·p3)·(p2+p4 – p2·p4).
Якщо п’ятий елемент виходить з ладу, то надійність системи – P(A/H2) – співпадає з надійністю системи, зображеної на мал.1.10.б). Скористаємося результатом прикладу 2.а) пункту 1.3.1:
P(A/H2) = p1·p2+p3·p4 – p1·p2·p3·p4.
Оскільки за умовою задачі P(H1) = p5 , а P(H2) =1– p5, то за допомогою формули повної ймовірності знаходимо:
P(A) = p5·(p1+p3 – p1·p3)·(p2+p4 – p2·p4)+(1 – p5)·(p1·p2+p3·p4 – p1·p2·p3·p4).
У тому випадку, коли всі елементи працюють з однаковою надійністю (pi=p): P(A) = p2·(2+2p – 5p2+2p3).
Зауваження. Припустимо, що деяка система може знаходитись в одному з станів E1, E2,...,En (наприклад, система, що складається з двох однотипних пристроїв, які відразу після виходу з ладу починають ремонтувати, може знаходитись в одному з чотирьох станів: E1 – обидва пристрої працюють, E2 – перший ремонтується, другий працює, E3 – другий ремонтується, перший працює, E4 – обидва ремонтується). Позначимо через Ek(s) подію, яка означає, що на момент часу s система знаходиться у стані Ek. Припустимо, що умовні ймовірності P(Ej(t+s)/Ek(s)) переходу системи із стану Ek в мо
мент часу s в стан Ej в момент часу t+s залежать тільки від тривалості проміжку часу [s; t+s] і не залежать від його положення на осі часу (мал.1.11). Назвемо ці умовні ймовірності перехідними ймовірностями системи і введемо позначення
P(Ej(t+s)/Ek(s)) = pkj(t), "s³0, t>0.
Скористаємося формулою повної ймовірності для виведення рівняння, якому задовольняють перехідні ймовірності.
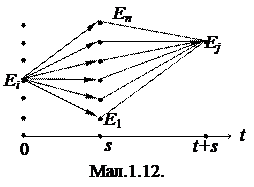Оскільки події E1(s), E2(s),..., En(s) складають повну систему, то перехід від стану Ei в момент часу 0 у стан Ej в момент часу t+s можна виконати n способами (мал.1.12):
Будемо вважати, що поведінка системи на проміжку часу [s; t+s] визначається її станом на момент часу s і не залежить від поведінки системи на проміжку часу [0; s]. Оскільки стан Ei системи у початковий момент часу не впливає на перехід системи із стану Ek в момент часу s в стан Ej в момент часу t+s, то
.
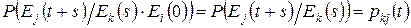Застосуємо тепер формулу повної ймовірності:
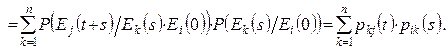
Таким чином, перехідні ймовірності задовольняють рівнянню Колмогорова-Чепмена
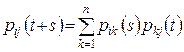. (6)
1.3.3. Теорема гіпотез (формули Бейєса)
Ця теорема є наслідком теореми множення ймовірностей.
Теорема. Нехай події Hk (k=1,...,n) утворюють повну систему подій (P(Hk)>0). Тоді для будь-якої події A (P(A)>0) виконується співвідношення
. (7)
Доведення. Оскільки 
, то на підставі формули (5) одержимо
.
Події Hk прийнято називати гіпотезами, P(Hk) - апріорними (відомими до проведення випробування), а P(Hk/A) - апостеріорними (обчисленими після випробування) ймовірностями цих гіпотез.
Приклад 1. В умовах прикладу 1 пункту 1.3.2 на приймальному кінці каналу одержано сигнал "0". Яка ймовірність того, що було послано сигнал "1"?
Розв’язок. Апріорна ймовірність гіпотези H1 (до випробування) дорівнює 1 – p0, а її апостеріорна ймовірність P(Hk/A) (після випробування) знаходиться за формулою (7)
.
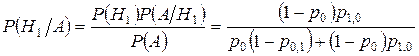Приклад 2. Надійність приладів (ймовірність безвідмовної роботи протягом заданого проміжку часу) в залежності від якості одного з елементів дорівнює відповідно 0.95, 0.9, 0.85. Відомо, що 30% приладів випускають у першому варіанті, 25% – у другому і 45% – у третьому. Довільно вибраний прилад безвідмовно працював протягом заданого проміжку часу. Яка ймовірність, що він був виконаний в кожному з варіантів?
Розв’язок. Позначимо через A подію, яка полягає у безвідмовній роботі приладу. Нехай гіпотеза Hk (k=1,...,n) означає, що прилад виконано у k-му варіанті. Тоді апріорні ймовірності гіпотез та умовні ймовірності A дорівнюють:
P(H1)=0.3, P(H2)=0.25, P(H3)=0.45,
P(A/H1)=0.95, P(A/H2)=0.9, P(A/H3)=0.85.
За формулою Бейєса знаходимо апостеріорні ймовірності гіпотез
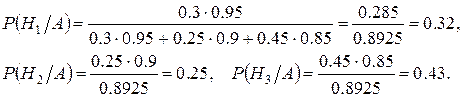
Приклад 3. Двоє стрільців роблять по одному пострілу. Ймовірність попадання по мішені для першого стрільця – 0.7, а для другого – 0.8. У мішені знайдено одну пробоїну. Яка ймовірність того, що у мішень попав перший стрілець?
Розв’язок. Подія A означає наявність однієї пробоїни в мішені. Введемо гіпотези H1 – обидва стрільці не попадають, H2 – перший стрілець попадає, другий ні, H3 – другий стрілець попадає, перший ні, H4 – обидва стрільці попадають. Знайдемо апріорні ймовірності гіпотез:
P(H1)=0.3·0.2=0.06, P(H2)=0.7·0.2=0.14,
P(H3)=0.3·0.8=0.24, P(H4)=0.7·0.8=0.56.
Умовні ймовірності події A дорівнюють:
P(A/H1)=0, P(A/H2)=P(A/H2)=1, P(A/H4)=0.
Таким чином, апостеріорна ймовірність гіпотези H2 така:
.