Плоскопаралельний хвилевід.
З розподілу компонент векторів поля (рис. 7.13) в площині фронту, раніше розглянутих неоднорідних хвиль  і
і  в (7.8) видно, що якщо ввести ряд площин, розміщених на відстанях
в (7.8) видно, що якщо ввести ряд площин, розміщених на відстанях
 , (7.79)
, (7.79)
від межі розділу, то для них будуть виконуватися умови  . Це означає, що якщо будь-яку з цих площин замінити ідеально провідними площинами, то порушення структури поля не відбудеться. Таким чином, ми переходимо до напрямляючої системи, яка утворена двома паралельними ідеально провідними площинами. В середині такої системи можуть існувати попередні
. Це означає, що якщо будь-яку з цих площин замінити ідеально провідними площинами, то порушення структури поля не відбудеться. Таким чином, ми переходимо до напрямляючої системи, яка утворена двома паралельними ідеально провідними площинами. В середині такої системи можуть існувати попередні  і
і  хвилі. Утворюються найпростіший порожниний хвилевід.
хвилі. Утворюються найпростіший порожниний хвилевід.
Якщо зафіксувати відстань між пластинами (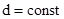 ), то можна визначити поперечне хвильове число
), то можна визначити поперечне хвильове число  , скориставшись для цього виразом (7.72):
, скориставшись для цього виразом (7.72):
 . (7.80)
. (7.80)
З (7.79) визначаємо 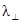 :
:
 . (7.81)
. (7.81)
Прирівнявши (7.80) і (7.81) визначимо  :
:
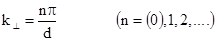 , (7.82)
, (7.82)
де n=0 має зміст тільки для горизонтальної поляризації (7.69) (7.70). Умова (7.82) показує, що для такого типу хвилеводу можливе існування безліч інших полів, крім розглянутих раніше  і
і  полів в 7.8. Послідовність значень поперечного хвильового числа
полів в 7.8. Послідовність значень поперечного хвильового числа  задовольняє розв’язкам (7.66–7.67) і (7.69–7.70), а також граничним умовам. Змінюючи n можна отримати різні тапи хвиль. На рис. 7.14 зображені розподіли
задовольняє розв’язкам (7.66–7.67) і (7.69–7.70), а також граничним умовам. Змінюючи n можна отримати різні тапи хвиль. На рис. 7.14 зображені розподіли  і
і  складових в площині фронту напрямляючої хвилі для вертикальної і горизонтальної поляризації.
складових в площині фронту напрямляючої хвилі для вертикальної і горизонтальної поляризації.
Отримаємо важливі параметри, характеризуючі розповсюдження хвилі в порожнинному хвилеводі. З виразу (7.71) можна отримати вираз для повздовжнього хвильового числа.
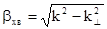 . (7.83)
. (7.83)
Тут k – хвильове число для необмеженого середовища з тими ж властивостями, що і середовище між площинами і воно дорівнює
 . (7.84)
. (7.84)
Виносячи k з під корення і враховуючи, що
 ,
,
приходимо до виразу
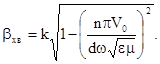
Введемо параметр  , який називається критичною частотою і яка дорівнює
, який називається критичною частотою і яка дорівнює
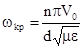 . (7.85)
. (7.85)
Остаточно, формула для повздовжнього хвильового числа буде мати вигляд з урахуванням (7.85):
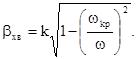 (7.86)
(7.86)
Звідси знаходиться фазова швидкість 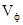 і довжина напрямляючої хвилі
і довжина напрямляючої хвилі 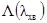 . Виходячи з (7.72) для визначення
. Виходячи з (7.72) для визначення 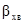 :
:
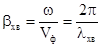 ,
,
маємо
 ; (7.87)
; (7.87)
 . (7.88)
. (7.88)
З виразу (7.87) і (7.88) видно, що 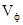 і
і 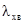 залежать від частоти, тобто розповсюдження напрямлених хвиль супроводжується дисперсією.
залежать від частоти, тобто розповсюдження напрямлених хвиль супроводжується дисперсією.
Висновки.
1. Фазова швидкість 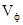 і довжина хвилі
і довжина хвилі 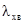 завжди більше відповідних величин в необмеженому середовищі:
завжди більше відповідних величин в необмеженому середовищі:
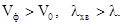
2. На частоті 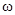 , яка дорівнює критичній
, яка дорівнює критичній 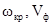 і
і 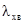 перетворюються в нескінченність. При цьому поле між площинами вже не буде хвилею, яка розповсюджується. Поле стає синфазним, тобто енергія не переноситься. Це стояча хвиля. Хвиля нормально падає на межі, кут падіння
перетворюються в нескінченність. При цьому поле між площинами вже не буде хвилею, яка розповсюджується. Поле стає синфазним, тобто енергія не переноситься. Це стояча хвиля. Хвиля нормально падає на межі, кут падіння 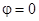 .
.
3. Хвиля буде напрямленою, якщо  . При цьому
. При цьому 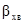 буде дійсною величиною. Це означає, що фазовий набіг буде змінюватися за лінійним законом при зміні координати Y, що являється ознакою рухомої хвилі.
буде дійсною величиною. Це означає, що фазовий набіг буде змінюватися за лінійним законом при зміні координати Y, що являється ознакою рухомої хвилі.
4. Якщо 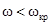 , то
, то 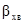 стає уявною величиною
стає уявною величиною
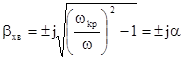 ,(7.89)
,(7.89)
тобто поле зберігає сталу фазу і в напрямку розповсюдження Y буде зменшуватися за експоненціальним законом
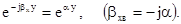 (7.89 а)
(7.89 а)
Умова (7.89) ще називають “умовою відсікання”. Вона виконується, як правило, для вищих n. Чим менше n, тим нижче 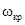 , при n=0 вона перетворюється в нуль. В цьому єдиному випадку буде розповсюджуватися плоска однорідна хвиля, у якої відсутня повздовжня складова.
, при n=0 вона перетворюється в нуль. В цьому єдиному випадку буде розповсюджуватися плоска однорідна хвиля, у якої відсутня повздовжня складова.
Розповсюдження напрямляючих хвиль в плоскому хвилеводі можна легко пояснити за допомогою багатократного відбиття від площин (рис. 7.15). На основі (7.71) і порівнянні з (7.86) отримаємо:
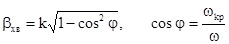 . (7.90)
. (7.90)
З рис. 7.15 видно, що при поступовому зменшенні кута падіння 
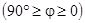 , зменшується частота
, зменшується частота 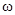 до
до 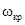 . При кутах падіння близьких до 90о, хвилі, відбиваючись від площин, розповсюджуються рівномірно, що можливо при високих частотах
. При кутах падіння близьких до 90о, хвилі, відбиваючись від площин, розповсюджуються рівномірно, що можливо при високих частотах  . Із зменшенням частоти
. Із зменшенням частоти 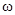 , збільшується
, збільшується  , тобто кут
, тобто кут  зменшується, а при
зменшується, а при 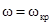 ,
, 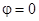 . При цьому хвиля розповсюджується нормально до площин хвилеводу. Енергія передаватися по хвилеводу не буде. Таким чином, хвилі
. При цьому хвиля розповсюджується нормально до площин хвилеводу. Енергія передаватися по хвилеводу не буде. Таким чином, хвилі  і
і  типу можуть формуватися на досить високих частотах (до
типу можуть формуватися на досить високих частотах (до 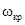 ). На низькихї частотах формується хвиля ТЕМ.
). На низькихї частотах формується хвиля ТЕМ.