Хвильові рівняння. Електродинамічні потенціали
5.1 Хвильові рівняння (рівняння Гельмгольця)
В електродинаміці існують два класи задач:
прямі задачі – необхідно визначити вектори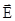 і
і 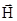 по відомим джерелам;
по відомим джерелам;
зворотні задачі – по заданому розподілу поля вимагається знайти його джерела;
Визначити вектори безпосередньо з рівнянь Максвела важко, тому їх необхідно перетворити так, щоб отримати диференційні рівняння більш зручні для розв’язку вказаних задач.
Вважаємо, що середовище являється лінійним, однорідним і ізотропним. Розглянемо систему рівнянь Максвела разом з матеріальними рівняннями. Візьмемо ротор від обох частин першого рівняння Максвела і змінимо порядок диференціювання за часом і координатами. Враховуючи співвідношення 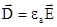 одержуємо
одержуємо
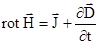 ,
,
 . (5.1)
. (5.1)
Ліву частину рівняння (5.1) перетворимо за допомогою відомої векторної тотожності
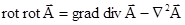 ,(5.2)
,(5.2)
де 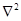 - оператор Лапласа.
- оператор Лапласа.
В декартовій системі координат оператор Лапласа має вигляд
 . (5.3)
. (5.3)
З урахуванням (5.2), (5.3) перепишемо рівняння (5.1) в формі
 . (5.4)
. (5.4)
Через те, що  , крім того
, крім того  , то (5.4) приймає вигляд
, то (5.4) приймає вигляд
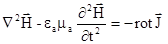 . (5.5)
. (5.5)
Рівняння (5.5) еквівалентне трьом скалярним рівнянням
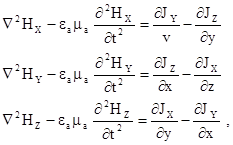 (5.6)
(5.6)
які відносяться до рівнянь вигляду
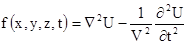 . (5.7)
. (5.7)
Такі рівняння (5.7) описують хвильові процеси і називаються неоднорідними хвильовими рівняннями, або неоднорідними рівняннями Даламбера. В них параметр V дорівнює швидкості хвильового процесу.
Якщо f (x, y, z, t)=0 – то це однорідні рівняння Даламбера. Рівняння (5.5) і (5.7) відрізняються тільки тим, що функції, які входять в (5.5) - векторні. Тому рівняння вигляду (5.5) - називаються неоднорідними векторними рівняннями Даламбера. Якщо права частина дорівнює нулю, то вони - однорідні векторні рівняння Даламбера.
Для вектору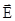 також можна вивести рівняння вигляду (5.4), взявши ротор від обох частин другого рівняння Максвела і виконавши аналогічні перетворення.
також можна вивести рівняння вигляду (5.4), взявши ротор від обох частин другого рівняння Максвела і виконавши аналогічні перетворення.
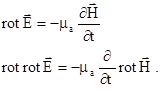 (5.8)
(5.8)
Враховуючи, що 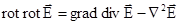 і вираз для Ñ2 (5.3), перепишемо рівняння (5.8) в вигляді
і вираз для Ñ2 (5.3), перепишемо рівняння (5.8) в вигляді
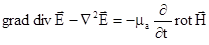 . (5.9)
. (5.9)
Через те, що  , а
, а  , то (5.9) приймає форму
, то (5.9) приймає форму
 (5.10)
(5.10)
В подальшому буде показане, що множник  , який входить в (5.4) і (5.10), являється аналогом параметру V в (5.7). Якщо середовище без втрат, то він відіграє роль швидкості розповсюдження електромагнітного поля і дорівнює швидкості світла V0 в середовищі, яке розглядається.
, який входить в (5.4) і (5.10), являється аналогом параметру V в (5.7). Якщо середовище без втрат, то він відіграє роль швидкості розповсюдження електромагнітного поля і дорівнює швидкості світла V0 в середовищі, яке розглядається.
Якщо в області, яка розглядається, є сторонні заряди і струми, то рівняння (5.5) і (5.10) будуть мати вигляд для векторів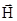 і
і 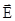
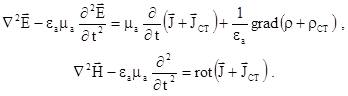 (5.11)
(5.11)
Вважаючи, що електромагнітні процеси встановилися, і середовище без втрат, в цьому випадку r=0, g=0,  , то отримаємо з (5.11)
, то отримаємо з (5.11)
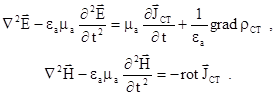 (5.12)
(5.12)
В випадку гармонійних полів, перейшовши у (5.12) до комплексних векторів, одержуємо
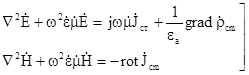 . (5.13)
. (5.13)
де  – комплексна магнітна і діелектрична проникність середовища.
– комплексна магнітна і діелектрична проникність середовища.
Якщо в області простору, яка розглядується будуть відсутні сторонні струми і заряди 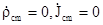 , то (5.13) спрощується, і остаточно отримаємо
, то (5.13) спрощується, і остаточно отримаємо
 , (5.14)
, (5.14)
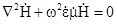 . (5.15)
. (5.15)
Рівняння вигляду (5.14) і (5.15) прийнято називати однорідними рівняннями Гельмгольца, а рівняння (5.13) – неоднорідними рівняннями Гельмгольца.
В рівняннях (5.14) і (5.15)  – комплексне число, яке являється сталою розповсюдження електромагнітної хвилі. В літературі цю величину називають хвильовим числомабо фазовою сталою. В подальшому ця величина буде розглянута детальніше.
– комплексне число, яке являється сталою розповсюдження електромагнітної хвилі. В літературі цю величину називають хвильовим числомабо фазовою сталою. В подальшому ця величина буде розглянута детальніше.
На підставі рівнянь (5.14) і (5.15) можна зробити важливий висновок теорії Максвела – зміна в часі електричного і магнітного полів неминуче призводить до розповсюдження в просторі електромагнітних хвиль з деякою сталою частотою.
В координатній формі рівняння Гельмгольца, наприклад, (5.14) записується слідуючим чином
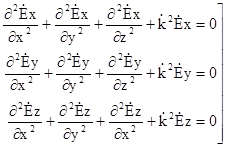 . (5.16)
. (5.16)
Розв’язок системи (5.16) значно спрощується, якщо поле не має яких-небудь складових, наприклад,  , а також, коли поле стале в будь-яких площинах, наприклад,
, а також, коли поле стале в будь-яких площинах, наприклад,
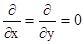 (5.17)
(5.17)