Векторний та скалярний потенціали. Вектор Герца
Хвильові рівняння (5.13), отримані в (5.1) застосовуються для визначення векторів електромагнітного поля, як правило, у випадку, якщо відсутні сторонні джерела, тобто коли ці рівняння однорідні – праві частини дорівнюють нулю. Якщо рівняння неоднорідні, тобто присутні праві частини, то розв’язок цих рівнянь ускладнено. Це пояснюються тим, що стороні струми і заряди входять в ці рівняння під знаком диференціальних операторів (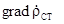
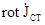 ).
).
Тому в електродинамці, для спрощення розв’язку практичних задач, вводять допоміжні функції, а потім через них обчислюють вектори 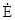 і
і  . Ці функції зв’язані з векторами
. Ці функції зв’язані з векторами 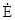 і
і  простими співвідношеннями, для яких праві частини рівнянь (5.13) мали не
простими співвідношеннями, для яких праві частини рівнянь (5.13) мали не 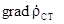 і
і 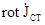 , а самі стороні заряди
, а самі стороні заряди  і стороні струми
і стороні струми 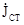 .
.
Такі допоміжні функції називаються електродинамічними потенціалами (скалярний потенціал 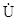 , векторний потенціал
, векторний потенціал 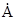 ).
).
У випадку гармонічних полів, рівняння Максвела мають вигляд:
 (5.18)
(5.18)
Отримаємо рівняння для векторного потенціалу 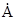 . Для цього скористаємося
. Для цього скористаємося четвертим рівнянням Максвела в системі (5.18). Так як дивергенція ротора будь якого вектора дорівнює нулю (
четвертим рівнянням Максвела в системі (5.18). Так як дивергенція ротора будь якого вектора дорівнює нулю ( ), то з четвертого рівняння Максвела слідує, що вектор
), то з четвертого рівняння Максвела слідує, що вектор  можна представити у вигляді ротора деякого вектора
можна представити у вигляді ротора деякого вектора 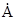 :
:
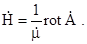 (5.19)
(5.19)
Векторну функцію 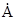 називають векторним електродинамічним потенціалом.
називають векторним електродинамічним потенціалом.
Підставимо рівність (5.19) в друге рівняння Максвела в (5.18):
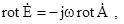
або
 (5.20)
(5.20)
З векторного аналізу відомо, що  , де
, де 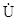 – будь-яка скалярна функція. Тому можна покласти, що
– будь-яка скалярна функція. Тому можна покласти, що
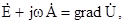
звідки
 (5.21)
(5.21)
Скалярну функцію 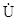 в (5.21) називають скалярним потенціалом. Знак “мінус” в (5.21) показує, що у випадку електростатичного поля функція
в (5.21) називають скалярним потенціалом. Знак “мінус” в (5.21) показує, що у випадку електростатичного поля функція 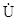 співпадає з звичайним виразом для електростатичного потенціалу.
співпадає з звичайним виразом для електростатичного потенціалу.
Підставляємо (5.19) і (5.21) в перше рівняння Максвела в системі (5.18):
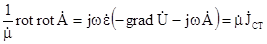 . (5.22)
. (5.22)
Помножимо (5.22) на 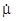 і скористаємося векторною тотожністю
і скористаємося векторною тотожністю
 (5.23)
(5.23)
для перетворення лівої частини рівності (5.22):
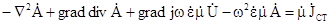 ,
,
або
 (5.24)
(5.24)
В вираз (5.24) входять дві невідомі функції 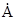 і
і 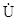 . Але, якщо накласти додаткову умову, яка пов’язуює потенціали
. Але, якщо накласти додаткову умову, яка пов’язуює потенціали 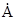 і
і 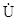 , яка називається умовою калібровки:
, яка називається умовою калібровки:
 (5.25)
(5.25)
то отримуємо рівняння відносно векторного потенціалу 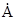 :
:
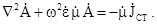 (5.26)
(5.26)
Аналогічне рівняння можна отримати для скалярного потенціалу 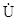 . Для цього необхідно підставити вираз для вектору
. Для цього необхідно підставити вираз для вектору 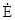 з (5.21) в третє рівняння Максвела в (5.18):
з (5.21) в третє рівняння Максвела в (5.18):
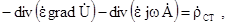
або
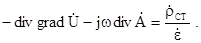 (5.27)
(5.27)
Використовуючи умову калібровки (5.25)  і тотожність
і тотожність  , приходимо до рівняння для скалярного потенціалу
, приходимо до рівняння для скалярного потенціалу 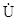 :
:
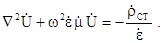 (5.28)
(5.28)
Таким чином, векторний  і скалярний
і скалярний  потенціали, як і вектори
потенціали, як і вектори 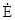 і
і  задовольняють неоднорідним рівнянням Гельмгольца. Однак праві частини рівнянь для потенціалів (5.26) і (5.28) мають більш простий вигляд.
задовольняють неоднорідним рівнянням Гельмгольца. Однак праві частини рівнянь для потенціалів (5.26) і (5.28) мають більш простий вигляд.
Умова калібровки (5.25) дозволяє виразити скалярну функцію 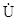 через векторний потенціал
через векторний потенціал 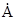 :
:
 (5.29)
(5.29)
Щоб встановити зв’язок поля з джерелом випромінювання, необхідно розв’язати рівняння (5.26) і (5.28). Найдемо частині розв’язки, вважаючи функції 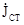 і
і  відомими в деякому об’ємі
відомими в деякому об’ємі  .
.
Згідно методу комплексних амплітуд множення на величину 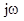 еквівалентне диференціюванню за часом
еквівалентне диференціюванню за часом 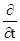 , то рівняння (5.26) і (5.28) можна переписати у вигляді:
, то рівняння (5.26) і (5.28) можна переписати у вигляді:
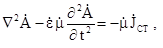 (5.30)
(5.30)
 (5.31)
(5.31)
Щоб знайти розв’язок (5.30) і (5.31) необхідно розглянути більш просту задачу доля статичного випадку. Будемо вважати, що  , а
, а  , аналогічно
, аналогічно 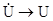 ,
, 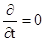 . Хвильові рівняння (5.30) і (5.31) вироджуються в рівняння Пуассона [3]:
. Хвильові рівняння (5.30) і (5.31) вироджуються в рівняння Пуассона [3]:
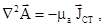 (5.32)
(5.32)
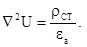 (5.33)
(5.33)
Розв’язки цих рівнянь детально приведені в [3]. Тут скористаємося кінцевим результатом:
 (5.34)
(5.34)
Цими формулами можна користуватися при квазістационарних процесах тобто процесах, які повільно змінюються за часом. Якщо 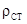 і
і 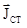 швидко змінюються, то необхідно враховувати запізнювання процесу при розповсюджені. Поле в точці спостереження М буде визначатися не за значенням
швидко змінюються, то необхідно враховувати запізнювання процесу при розповсюджені. Поле в точці спостереження М буде визначатися не за значенням  і
і 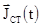 в даний момент часу а більш ранніми значеннями
в даний момент часу а більш ранніми значеннями 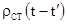 і
і 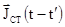 , де
, де 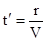 , тобто це час, за який поле розповсюдилось від джерела до точки спостереження. Якщо опустити суворе доведення розв’язку, з яким можна детально ознайомитися в [3], то розв’язки можна визначити як
, тобто це час, за який поле розповсюдилось від джерела до точки спостереження. Якщо опустити суворе доведення розв’язку, з яким можна детально ознайомитися в [3], то розв’язки можна визначити як
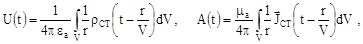 (5.35)
(5.35)
де 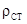 і
і 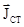 зв’язані рівнянням неперервності:
зв’язані рівнянням неперервності:

Формули (5.35) називаються запізнювальними потенціалами.
Для гармонічного за часом процесу замість
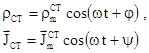
під знаком інтегралів (5.35), необхідно записати
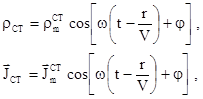
або
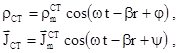
де 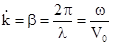 – стала розповсюдження у вільному просторі.
– стала розповсюдження у вільному просторі.
Якщо вважать, що середовище з втратами, то в комплексній формі вирази для амплітуд запізнювальних потенціалів 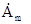 і
і 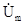 будуть мати вигляд
будуть мати вигляд
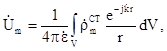 (5.36)
(5.36)
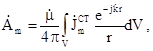 (5.37)
(5.37)
де  – комплексна амплітуда вектора
– комплексна амплітуда вектора  ;
;
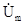 – комплексна амплітуда скалярного потенціалу
– комплексна амплітуда скалярного потенціалу 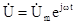 ;
;
r – відстань від елементарного об’єму 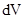 до точки спостереження М;
до точки спостереження М;
 – комплексна стала розповсюдження.
– комплексна стала розповсюдження.
Вирази (5.36) і (5.37) являються частинними розв’язками рівнянь (5.30) і (5.31) і представляють собою сферичні хвилі, які розходяться від джерела. Фронт хвилі – кульова поверхня, радіус якої зростає з швидкістю V.
Часто для наближених розрахунків об’ємне розподілення зарядів і струмів замінюють їх поверхневим розподілом 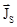 . В цьому випадку
. В цьому випадку
 (5.38)
(5.38)
У випадку лінійного стороннього струму  , комплексна амплітуда векторного потенціалу
, комплексна амплітуда векторного потенціалу  буде виражатися формулою:
буде виражатися формулою:
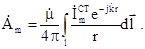 (5.39)
(5.39)
Крім електродинамічних потенціалів 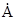 і
і 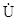 , використовують інші потенціали, наприклад, вектор Герца (
, використовують інші потенціали, наприклад, вектор Герца (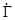 ). Цей вектор зв’язаний з потенціалами
). Цей вектор зв’язаний з потенціалами 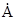 і
і 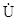 співвідношеннями
співвідношеннями
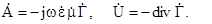 (5.40)
(5.40)
Хвильове рівняння для комплексного вектора Герца [3] буде мати вигляд:
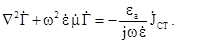 (5.41)
(5.41)
Комплексна амплітуда вектора Герца ( ) в результаті розв’язку рівняння (5.41) буде дорівнювати
) в результаті розв’язку рівняння (5.41) буде дорівнювати
 (5.42)
(5.42)