Параметр в загальному випадку комплексна величина
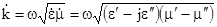 (6.11)
(6.11)
і називається хвильовим числом.
Через те, що рівняння (6.10) залежить від однієї координати z, перпендикулярної плоским хвильовим поверхням, то в (6.10) частинні похідні замінимо повними
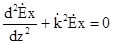 . (6.13)
. (6.13)
Диференційне рівняння (6.13) другого порядку для 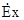 має розв’язок у вигляді суперпозиції двох частинних розв’язків виду
має розв’язок у вигляді суперпозиції двох частинних розв’язків виду
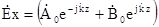 , (6.14)
, (6.14)
де 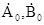 – довільні сталі інтегрування, які представляють собою комплексні амплітуди, наприклад,
– довільні сталі інтегрування, які представляють собою комплексні амплітуди, наприклад, 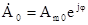 ; які визначаються з граничних умов. Підставивши розв’язок (6.14) в (6.6), отримаємо
; які визначаються з граничних умов. Підставивши розв’язок (6.14) в (6.6), отримаємо
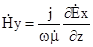 , (6.15)
, (6.15)
звідки
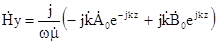 ,
,
або
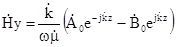 . (6.16)
. (6.16)
Враховуючи, що 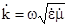 , тоді (6.16) приймає вигляд
, тоді (6.16) приймає вигляд
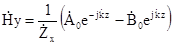 , (6.17)
, (6.17)
де
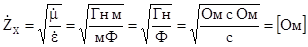 . (6.18)
. (6.18)
Величина 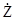 вимірюється в омах і називається характеристичним опором середовища. В загальному випадку
вимірюється в омах і називається характеристичним опором середовища. В загальному випадку 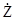 величина комплексна. В середовищі без втрат
величина комплексна. В середовищі без втрат 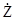 величина дійсна:
величина дійсна:
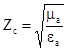 . (6.19)
. (6.19)
Для вакууму 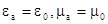 ,
,
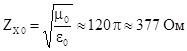 . (6.20)
. (6.20)
Аналогічно виконавши операції, зроблені для 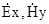 , можна отримати розв’язок для
, можна отримати розв’язок для 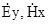 .
. 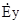 з (6.9) буде дорівнювати
з (6.9) буде дорівнювати
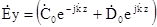 , (6.21)
, (6.21)
а 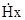 , використовуючи (6.21) і (6.9) буде дорівнювати
, використовуючи (6.21) і (6.9) буде дорівнювати
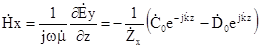 . (6.22)
. (6.22)
В середовищі без втрат (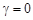 ), стала розповсюдження - величина дійсна
), стала розповсюдження - величина дійсна 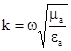 , тоді переходячи від комплексних амплітуд до миттєвих значень, знайдемо
, тоді переходячи від комплексних амплітуд до миттєвих значень, знайдемо
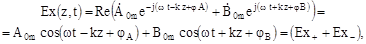 (6.23)
(6.23)
де 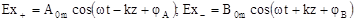 .
.
Вираз (6.23) описує плоску електромагнітну хвилю, причому 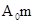 – її амплітуда, а аргумент косинуса – повна фаза
– її амплітуда, а аргумент косинуса – повна фаза 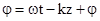 змінюється в часі і просторі, а отже, змінюється і положення фазового фронту. Залежність Ex від z в фіксований моменти часу
змінюється в часі і просторі, а отже, змінюється і положення фазового фронту. Залежність Ex від z в фіксований моменти часу 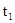 та
та 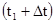 зображена на рис. 6.1
зображена на рис. 6.1
Знайдемо швидкість переміщення фронту хвилі, для чого зафіксуємо фазу поля 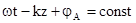 і
і 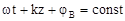 . Продиференціювавши ці рівності за часом, отримаємо
. Продиференціювавши ці рівності за часом, отримаємо
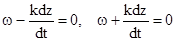 .
.
Звідси фазова швидкість
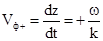 і
і 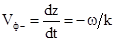 . (6.24)
. (6.24)
Таким чином, складова 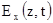 представляє собою суперпозицію двох незалежних одна від одної рухомих хвиль, одна з яких
представляє собою суперпозицію двох незалежних одна від одної рухомих хвиль, одна з яких 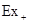 розповсюджується в напрямку зростаючих значень z з фазовою швидкістю
розповсюджується в напрямку зростаючих значень z з фазовою швидкістю 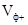 , і називається падаючю, а інша – в напрямку зменшення значень z зі швидкістю
, і називається падаючю, а інша – в напрямку зменшення значень z зі швидкістю 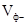 – і називається відбитою.
– і називається відбитою.
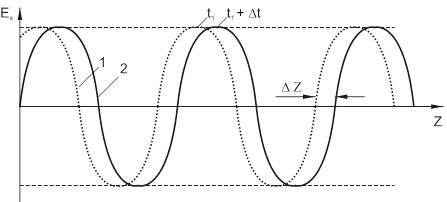
Рисунок 6.1
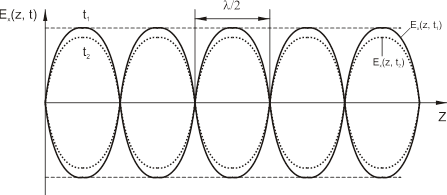
Рисунок 6.2
Поки що, будемо розглядати тільки падаючу хвилю, тому можна записати, опускаючи знак “+”, що
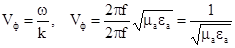 . (6.25)
. (6.25)
Для вакууму
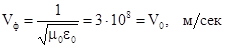 – швидкість світла. (6.27)
– швидкість світла. (6.27)
З (6.25) слідує співвідношення, яке зв’язує хвильове число та частоту у вільному просторі
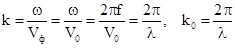 , (6.28)
, (6.28)
враховуючи, що 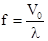 .
.
Вираз (6.28), називається сталою розповсюдження електромагнітної хвилі у вільному просторі 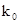 .
.
Використовуючи форму запису (6.23) переходу від комплексних амплітуд до миттєвих значень складової 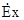 , можна представити інші компоненти поля
, можна представити інші компоненти поля 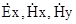 у вигляді
у вигляді
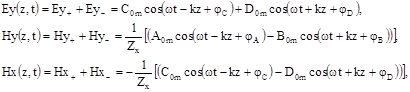 (6.29)
(6.29)
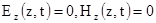 . (6.30)
. (6.30)
Отже, електромагнітне поле (6.23) і (6.29) представляє собою суперпозицію чотирьох незалежних рухомих хвиль, які визначаються 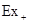 і
і 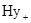 ,
, 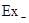 і
і 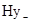 ,
, 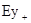 і
і 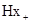 ,
, 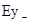 і
і 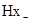 . Однорідні плоскі рухомі хвилі (6.23) і (6.29) розповсюджуються вздовж осі z, яка перпендикулярна їхнім хвильовим площинам. Згідно з (6.30) вектори
. Однорідні плоскі рухомі хвилі (6.23) і (6.29) розповсюджуються вздовж осі z, яка перпендикулярна їхнім хвильовим площинам. Згідно з (6.30) вектори  і
і  цих хвиль лежать в хвильових площинах і представляють собою поперечні складові векторів поля по відношенню до напрямку розповсюдження.
цих хвиль лежать в хвильових площинах і представляють собою поперечні складові векторів поля по відношенню до напрямку розповсюдження.
Якщо, зокрема, амплітуда падаючої і відбитої хвиль рівні одна одній і дорівнюють початковій фази, то отримуємо стоячу хвилю. Наприклад, для 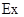 складової:
складової:
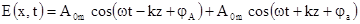 ,
,
використовуючи відому тригонометричну тотожність
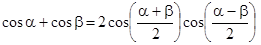 ,
,
отримуємо
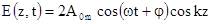 . (6.31)
. (6.31)
Як видно (рис. 6.3) в кожний момент часу маємо нерухому косинусоїду: її нулі не зміщуються вздовж осі z, а залишаються фіксованими. Отже, все сказане можна стисло записати рівняннями, які зв’язують компоненти поля плоскої хвилі, для середовища з втратами
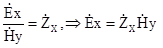 , (6.32)
, (6.32)
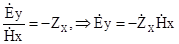 . (6.33)
. (6.33)
Розповсюдження хвилі супроводжується переносом потужності. Комплексний вектор Пойнтинга має тільки дійсну частину
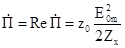 , (6.34)
, (6.34)
де
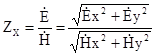 . (6.35)
. (6.35)
При довільному напрямку розповсюдження електромагнітної хвилі вздовж r, розв’язок рівняння Гемгольца можна записати
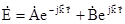 , (6.36)
, (6.36)
де 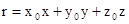 – радіус-вектор довільної точки спостереження;
– радіус-вектор довільної точки спостереження;
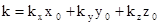 – хвильовий вектор, перпендикулярний до хвильового фронту.
– хвильовий вектор, перпендикулярний до хвильового фронту.