Граничні умови для векторів електричного поля
А. Нормальні складові. Вектор електричної індукції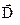 підлягає наступній граничній умові:
підлягає наступній граничній умові:
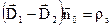 , або
, або 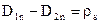 . (3.3)
. (3.3)
Вираз (3.3) показує, що при переході з одного середовища в інше, нормальна компонента вектора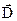 має стрибок, який дорівнює поверхневій густині заряду
має стрибок, який дорівнює поверхневій густині заряду  , розподіленого вздовж межі розділу. Якщо
, розподіленого вздовж межі розділу. Якщо 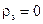 , то нормальна компонента вектора
, то нормальна компонента вектора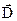 залишається неперервною при переході з одного середовища в інше:
залишається неперервною при переході з одного середовища в інше:
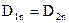 при
при 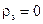 , (3.4)
, (3.4)
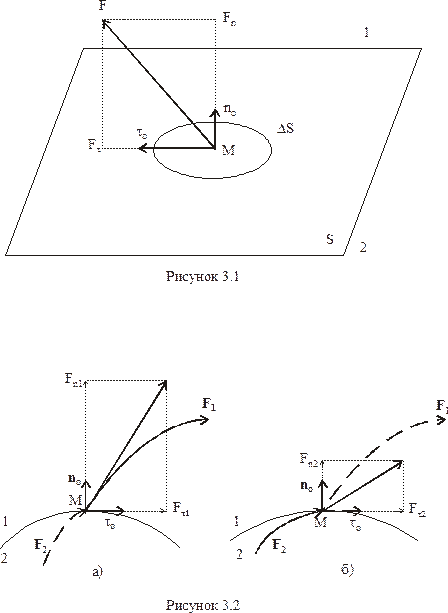
де 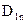 і
і 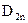 проекції векторів
проекції векторів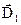 і
і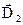 на нормаль
на нормаль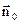 .
.
Вивід. Доведення будується на застосуванні третього рівняння Максвела в інтегральній формі. На поверхні розділу двох середовищ з параметрами 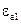 і
і 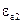 виділимо достатньо малий елемент
виділимо достатньо малий елемент 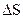 (рис. 3.3), щоб його можна було вважати плоским. Побудуємо на елементі
(рис. 3.3), щоб його можна було вважати плоским. Побудуємо на елементі 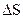 прямий циліндр висотою
прямий циліндр висотою 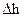 так, щоб його основи були в різних середовищах. Через малі розміри циліндра поле на його основах можна вважати однорідним:
так, щоб його основи були в різних середовищах. Через малі розміри циліндра поле на його основах можна вважати однорідним: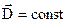 . Зовнішня нормаль до верхньої основи напрямлена по
. Зовнішня нормаль до верхньої основи напрямлена по 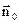 , а до нижньої – протилежно
, а до нижньої – протилежно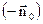 . Поверхню циліндра можна представити у вигляді
. Поверхню циліндра можна представити у вигляді 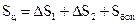 , де
, де 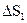 і
і 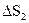 – площі верхньої і нижньої основи, а
– площі верхньої і нижньої основи, а 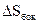 – бокова поверхня. Тоді рівняння Максвела можна переписати
– бокова поверхня. Тоді рівняння Максвела можна переписати
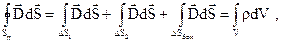 (3.5)
(3.5)
де 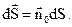
Спрямуємо висоту циліндра 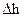 до нуля так, щоб його основи залишалися в різних середовищах. При цьому в границі
до нуля так, щоб його основи залишалися в різних середовищах. При цьому в границі 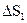 і
і 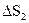 збігаються з
збігаються з 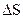 . Через те, що елемент
. Через те, що елемент 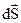 в (3.5) збігається за напрямком з зовнішньою нормаллю до поверхні
в (3.5) збігається за напрямком з зовнішньою нормаллю до поверхні 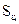 , то в результаті граничного переходу, отримаємо:
, то в результаті граничного переходу, отримаємо:
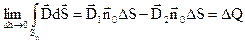 , (3.6)
, (3.6)
де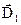 і
і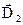
 – значення вектора
– значення вектора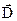 на межі розділу в першому і другому середовищі відповідно.
на межі розділу в першому і другому середовищі відповідно.
В (3.6) при 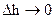 зник потік через
зник потік через 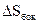 , а також стає рівним нулю об’єм, то зникає і та частина заряду, яка могла б бути розподілена в ньому, тобто залишається тільки заряд, який зосереджений на межі розділу. Якщо розділити обидві частини рівності (3.6) на
, а також стає рівним нулю об’єм, то зникає і та частина заряду, яка могла б бути розподілена в ньому, тобто залишається тільки заряд, який зосереджений на межі розділу. Якщо розділити обидві частини рівності (3.6) на 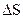 , отримаємо
, отримаємо
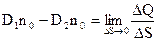 ,
,
або
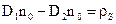 .
.
Бачимо, що ця рівність повністю співпадає з (3.3).
Якщо в (3.3) виразити 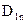 і
і 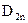 через
через 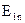 і
і 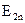 за допомогою рівності
за допомогою рівності 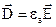 , отримаємо граничну умову для нормальних компонент вектора
, отримаємо граничну умову для нормальних компонент вектора  :
:
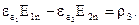 (3.7)
(3.7)
Якщо 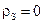 , то
, то
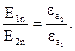 (3.8)
(3.8)
Б. Дотичні тангенціальні складові. Для дотичних складових вектора гранична умова має вигляд
гранична умова має вигляд
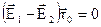 , або
, або  . (3.9)
. (3.9)
Рівність (3.9) показує, що дотичні складові вектора при переході через межу розділу двох середовищ неперервна. Напрямок орту
при переході через межу розділу двох середовищ неперервна. Напрямок орту 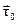 може змінюватися (рис. 3.1), тому більш зручно зробити запис через орт
може змінюватися (рис. 3.1), тому більш зручно зробити запис через орт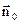 , через те, що його напрямок вибирається однозначно, тоді
, через те, що його напрямок вибирається однозначно, тоді
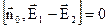 . (3.10)
. (3.10)
Вивід. Геометрія задачі: перетнемо межову поверхню S площиною Р, яка проходить через нормаль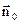 до S (рис. 3.4).
до S (рис. 3.4).
На лінії перетину поверхні розділу і площини Р виділимо достатньо малий відрізок 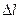 так, щоб точка, яка розглядається знаходилась в середині цього відрізка. Розміри
так, щоб точка, яка розглядається знаходилась в середині цього відрізка. Розміри 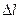 повинні бути такими, щоб його можна було вважати прямолінійним.
повинні бути такими, щоб його можна було вважати прямолінійним.
На відрізку 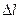 побудуємо прямокутний контур ABCD висоти
побудуємо прямокутний контур ABCD висоти 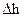 , щоб він знаходився в обох середовищах.
, щоб він знаходився в обох середовищах.
Проведемо додатковий орт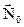 перпендикулярний до площини Р і одиничну дотичну
перпендикулярний до площини Р і одиничну дотичну 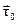 до відрізка
до відрізка 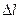 . Всі три орта
. Всі три орта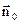 ,
, 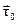 ,
, 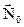 зв'язані співвідношенням
зв'язані співвідношенням
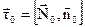 , (3.11)
, (3.11)
і складають праву трійку векторів.
Вивід базується на застосуванні другого рівняння Максвела в інтегральній формі, причому в якості контуру 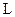 в ньому, вибираємо контур ABCD. Через його малі розміри, поле на сторонах АВ і СD можна вважати однорідним:
в ньому, вибираємо контур ABCD. Через його малі розміри, поле на сторонах АВ і СD можна вважати однорідним: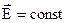 . Напрямок обходу контуру беремо як вказане на рис. 3.4. Тому можна записати
. Напрямок обходу контуру беремо як вказане на рис. 3.4. Тому можна записати
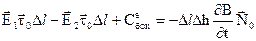 , (3.12)
, (3.12)
де 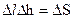 – площа, яка охоплюється контуром.
– площа, яка охоплюється контуром.

В границі при 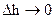 сторони AB і CD збігаються на межі S з
сторони AB і CD збігаються на межі S з 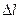 ; при цьому
; при цьому 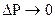 :
: 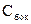 і права частина (3.12) зникають. Відкидаючи спільний множник
і права частина (3.12) зникають. Відкидаючи спільний множник 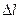 , формально приходимо до (3.9)
, формально приходимо до (3.9)
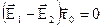 .
.
Ця рівність справедлива для будь-якого напрямку 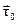 на S.
на S.
Щоб отримати граничні умови в формі (3.10) замінимо 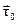 в (3.10) через
в (3.10) через 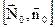 , а потім врахувавши властивість змішаного добутку векторів, отримаємо:
, а потім врахувавши властивість змішаного добутку векторів, отримаємо:
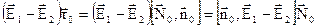 .
.
Через те, що орт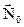 , який задає орієнтацію площини Р являється невизначеним, отримаємо
, який задає орієнтацію площини Р являється невизначеним, отримаємо
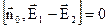 ,
,
що співпадає з (3.10).
Дотична складова вектору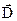 , навпаки, має розрив, величина, якого складає відношення діелектричних проникностей середовищ
, навпаки, має розрив, величина, якого складає відношення діелектричних проникностей середовищ
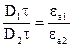 . (3.13)
. (3.13)
Виведені граничні умови показують, що вектори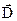 і
і на межі розділу заломлюються. Проілюструємо це на прикладі (рис. 3.5). Позначимо кути між нормаллю
на межі розділу заломлюються. Проілюструємо це на прикладі (рис. 3.5). Позначимо кути між нормаллю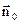 до поверхні розділу і векторами
до поверхні розділу і векторами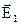 і
і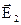 відповідно через
відповідно через 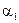 і
і 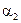 . Через те, що
. Через те, що 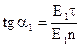 , а
, а 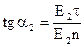 , то використовуючи граничні умови (3.9) і (3.8), отримуємо, що при відсутності поверхневих зарядів на межі розділу справедливе наступне співвідношення:
, то використовуючи граничні умови (3.9) і (3.8), отримуємо, що при відсутності поверхневих зарядів на межі розділу справедливе наступне співвідношення:
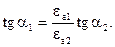 (3.14)
(3.14)
В ізотропних середовищах вектори  і
і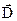 напрямлені однаково. Тому (3.14) справедливо для вектору
напрямлені однаково. Тому (3.14) справедливо для вектору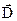 .
.