Таблиця 2.1
| Інтегральна форма | Диференційна форма | ||
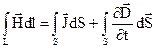
| 
| ||
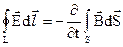
| 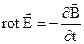
| ||

| 
| ||

| 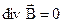
| ||
| Матеріальні рівняння | |||
5. 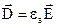 6. 6. 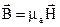 7. 7. 
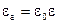 , , 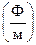  , ,   
| |||
| Наслідок рівнянь Максвела | |||
Закон збереження заряду
8. 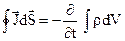 або або
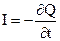
| Рівняння неперервності
9.  або або
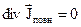
| ||
В таблиці 2.1 приведені рівняння, які складають основу теорії електромагнетизму. Всі величини, які входять в ці рівняння, є функції координат і часу t. Частіше всього, при розв’язку задач електродинаміки, використовують рівняння Максвела в диференційній формі. Операції rot і div в них – це комбінації частинних похідних першого порядку від проекцій векторних полів у відповідній системі координат. Зауважимо, що достатньо знайти один електричний вектор, наприклад  , або один магнітний вектор, наприклад,
, або один магнітний вектор, наприклад, 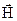 і скориставшись матеріальними рівняннями (табл. 2.1) можна отримати два останніх вектора
і скориставшись матеріальними рівняннями (табл. 2.1) можна отримати два останніх вектора 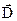 і
і  .
.
2.2 Перше рівняння Максвела (узагальнення закону Ампера)
Датський фізик Ерстед встановив експериментальний факт, що протікання струму по провідниках приводить до виникнення магнітного поля. Французький фізик Ампер на основі відкриття Ерстеда сформулював закон повного струму, який називається законом Ампера.
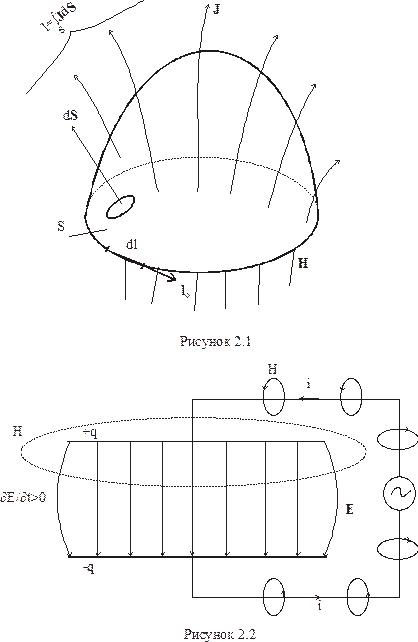
Інтегральна форма закону Ампера: розглянемо в просторі контур 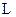 , обмежений поверхнею
, обмежений поверхнею  (рис. 3.1). Напрям обходу контуру вибираємо таким чином, щоб під час руху вздовж контуру з кінця вектора елементарної площинки
(рис. 3.1). Напрям обходу контуру вибираємо таким чином, щоб під час руху вздовж контуру з кінця вектора елементарної площинки  , він був проти часової стрілки. Припустимо, що поверхня
, він був проти часової стрілки. Припустимо, що поверхня  пронизується деякою системою струмів, розподілених в просторі неперервно з деякою об’ємною густиною
пронизується деякою системою струмів, розподілених в просторі неперервно з деякою об’ємною густиною  . Тоді повний струм, який пронизує контур, визначиться у вигляді:
. Тоді повний струм, який пронизує контур, визначиться у вигляді:
 . (2.1)
. (2.1)
Закон повного струму: циркуляція по контуру 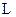 напруженості магнітного поля
напруженості магнітного поля 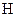 , спричинена протіканням
, спричинена протіканням  , дорівнює повному струму
, дорівнює повному струму
 . (2.2)
. (2.2)
Підставимо формулу (2.2) в (2.1), і тоді отримуємо інтегральну форму закону Ампера
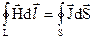 . (2.3)
. (2.3)
Диференційна форма закону Ампера. Якщо скористатися теоремою Стокса для будь-якого векторного поля
 , (2.4)
, (2.4)
і з її допомогою перетворити вираз (2.3), то будемо мати:
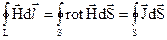 , (2.5)
, (2.5)
через те, що контур довільний, то рівність (2.5) можлива при умові:
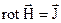 . (2.6)
. (2.6)
Рівняння (2.6) це – диференційна форма закону Ампера. Закон Ампера справедливий у випадку постійних процесів і виявляється невірним у випадку змінних процесів. Максвел дав узагальнююче формулювання закону повного струму. Він ввів поняття струму зміщення, який з точки зору утворення магнітного поля, рівноцінний струму провідності.
Прикладом системи зі струмами зміщення може бути конденсатор в колі змінного струму (рис. 2.2). Змінний електричний струм протікає по замкнутому колу, в якому є конденсатор, незважаючи на те, що між обкладинками відсутні носії електричного заряду. Тобто там протікає якийсь струм по природі відмінний від струму провідності. Цей струм називається струмом зміщення. З’єднувальний провід оточений кільцевими лініями магнітного поля. Максвел припустив, що вони не обриваються у пластин конденсатора, а утворюють замкнену поверхню, тобто змінне електричне поле також
оточене магнітним полем. Це дало основу для введення поняття про новий вид струму – струму зміщення Jзм 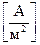 .
.
Густина струму зміщення визначається формулою:
 . (2.7)
. (2.7)
Підкреслимо: струм провідності – впорядкований рух вільних електричних зарядів. Струм зміщення – відповідає тільки зміні електричного поля і не супроводжується яким-небудь рухом електричних зарядів.
У вакуумі 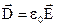 і (2.7) приймає вид:
і (2.7) приймає вид:
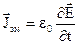 . (2.8)
. (2.8)
Струм зміщення у вакуумі не супроводжується зміною тепла.
І так, у випадку змінного поля, Максвел запропонував додати у праву частину закону Ампера струм зміщення, щоб він був вірний для цього. Тоді
 . (2.9)
. (2.9)
Струм зміщення виражається через густину струму зміщення
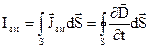 . (2.10)
. (2.10)
Тепер, якщо підставити (2.10), (2.1) в (2.9), отримуємо
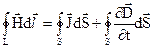 . (2.11)
. (2.11)
Рівняння (2.11) сформульоване для контуру скінчених розмірів. Це перше рівняння Максвела в інтегральній формі.
Для переходу до диференційної форми, необхідно скористатися теоремою Стокса. Тоді отримуємо:
 . (2.12)
. (2.12)
Через те, що  – довільна поверхня, то (2.12) можливо тільки в тому випадку, якщо
– довільна поверхня, то (2.12) можливо тільки в тому випадку, якщо
 . (2.13)
. (2.13)
Рівняння (2.13) – це диференційна форма першого рівняння Максвела.
Вираз (2.13) встановлює внутрішній взаємозв’язок електричного і магнітного поля. Зміна в часі електричного поля в який-небудь точці простору приводить до виникнення струму зміщення, який викликає появу змінного магнітного поля.
Векторне рівняння (2.13) в диференційній формі еквівалентне трьом скалярним рівнянням, які в декартовій системі координат мають вигляд:
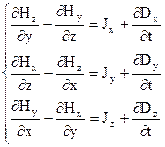 (2.14)
(2.14)
2.3 Друге рівняння Максвела (узагальнений закон електромагнітної індукції)
Друге рівняння є узагальненням закону індукції Фарадея: якщо замкнений контур 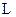 пронизується змінним струмом
пронизується змінним струмом 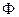 , то в контурі виникає ЕРС, яка дорівнює швидкості зміни магнітного потоку (рис. 2.3):
, то в контурі виникає ЕРС, яка дорівнює швидкості зміни магнітного потоку (рис. 2.3):
 . (2.15)
. (2.15)
Знак “мінус” в правій частині (2.15) означає, що ЕРС нібито прагне перешкодити зміні потоку 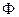 , який пронизує цей контур. Це положення відоме як “правило Лоренца”. Це рівняння справедливо тільки для провідного контуру. Максвел припустив, що це рівняння справедливе також і в тому випадку, якщо середовище не має провідність. Відомо, що будь-яка ЕРС, яка наводиться на контур і, дорівнює циркуляції вектора
, який пронизує цей контур. Це положення відоме як “правило Лоренца”. Це рівняння справедливо тільки для провідного контуру. Максвел припустив, що це рівняння справедливе також і в тому випадку, якщо середовище не має провідність. Відомо, що будь-яка ЕРС, яка наводиться на контур і, дорівнює циркуляції вектора 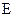 по цьому контуру:
по цьому контуру:
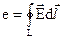 . (2.16)
. (2.16)
Магнітний струм 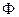 зв’язаний з вектором
зв’язаний з вектором  співвідношенням
співвідношенням
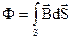 , (2.17)
, (2.17)
де  – довільна поверхня, яка опирається на контур
– довільна поверхня, яка опирається на контур 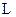 ;
;
 ,
, 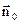 – орт нормалі до поверхні
– орт нормалі до поверхні  , який утворює правогвинтову систему з обходом контуру (2.13).
, який утворює правогвинтову систему з обходом контуру (2.13).
Підставляючи формули (2.17) і (2.16) в (2.15), отримуємо
 . (2.18)
. (2.18)
Це співвідношення (2.18) придатне для контуру скінчених розмірів і називається другим рівнянням Максвела в інтегральній формі.
Диференційна форма. Якщо вважати, що контур нерухомий і не змінюється з часом, тоді можливо похідну по часі внести під знак інтеграла (2.18)
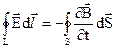 . (2.19)
. (2.19)
Застосовуючи теорему Стокса
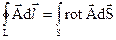 ,
,
можна переписати (2.19) у вигляді
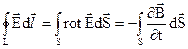 . (2.20)
. (2.20)
Через те, що  – довільна поверхня, то (2.20) виконується у випадку, якщо
– довільна поверхня, то (2.20) виконується у випадку, якщо
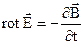 . (2.21)
. (2.21)
Співвідношення (2.21) – це диференційна форма другого рівняння Максвела.
В прямокутній системі координат  отримуємо три скалярних рівняння:
отримуємо три скалярних рівняння:
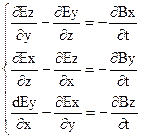 . (2.22)
. (2.22)
З (2.21) слідує, що ротор напруженості електричного поля  в будь-який його точці дорівнює по величині і протилежний за знаком швидкості зміни індукції
в будь-який його точці дорівнює по величині і протилежний за знаком швидкості зміни індукції  в цій точці.
в цій точці.
2.4 Третє рівняння Максвела (узагальнена теорема Гауса)
Закон Гауса встановлює зв’язок між векторним полем  і величиною заряду, який його породжує. Розглянемо деякий об’єм
і величиною заряду, який його породжує. Розглянемо деякий об’єм 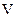 , обмежений замкненою поверхнею
, обмежений замкненою поверхнею  (рис. 2.4, а). В середині об’єму знаходиться електричний заряд
(рис. 2.4, а). В середині об’єму знаходиться електричний заряд 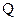 . Математично теорема Гауса формулюється
. Математично теорема Гауса формулюється
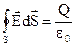 . (2.23)
. (2.23)
Потік вектора  через поверхню
через поверхню  чисельно дорівнює заряду поділеному на
чисельно дорівнює заряду поділеному на  . Якщо заряд розподілений неперервно, то
. Якщо заряд розподілений неперервно, то 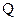 визначається як
визначається як
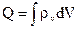 , (2.24)
, (2.24)
де 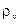 – об’ємна густина заряду.
– об’ємна густина заряду.
Підставив (2.24) в (2.23) маємо
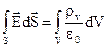 , (2.25)
, (2.25)
Вираз (2.25) можна записати в іншому виді, якщо використати матеріальне рівняння 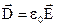 :
:
 . (2.26)
. (2.26)
Рівняння (2.26) – це третє рівняння Максвела в інтегральній формі.
Диференційна форма. Використовуючи результат теореми Остроградського-Гауса
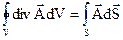 , (2.27)
, (2.27)
отримаємо
 . (2.28)
. (2.28)
Ця рівність виконується при будь-якому об’ємі, а це можливе тільки в тому випадку, якщо
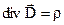 . (2.29)
. (2.29)
Співвідношення (2.29) – це третє рівняння Максвела в інтегральній формі.
З (2.29) слідує, що дивергенція вектора 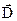 відміна від нуля тільки в тих точках простору, де є вільні заряди. В цих точках лінії вектора
відміна від нуля тільки в тих точках простору, де є вільні заряди. В цих точках лінії вектора 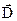 мають початок (витік) (рис. 2.4, б) і кінець (стік) (рис. 2.4, в). Лінії вектора
мають початок (витік) (рис. 2.4, б) і кінець (стік) (рис. 2.4, в). Лінії вектора 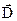 починаються на позитивних зарядах і закінчуються на негативних. Такі поля називаються потенційними.
починаються на позитивних зарядах і закінчуються на негативних. Такі поля називаються потенційними.
В прямокутній системі координат рівняння (2.29) записується у вигляді
 . (2.30)
. (2.30)