Решение.

Окончательный ответ всегда старайтесь максимально упростить, это может очень облегчить жизнь в дальнейшем.

При достаточной натренированности нужда в записи цепочки сложности и выписывании промежуточных аргументов, по которым вычисляется очередная функция, отпадает, но в начале изучения советуем использовать ее в качестве подручного средства (кстати, этот прием был придуман вместе со студентами-заочниками и успешно используется уже много лет).

Итак, мы разобрали случай, когда функция задана одним, хотя и сложным, выражением.

Если величина является арифметическим действием нескольких сложных функций, то здесь действует правило: действие – сложность – формула. Покажем это на примерах.

Пример 12.5. Вычислить производную функции

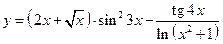Решение. Главное действие – разность, два других – произведение и частное. Сложные функци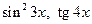и: и 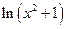. Их производные можно найти заранее, а потом просто вставить в ответ, а можно решать по тексту. Для первого примера вычислим их производные отдельно.

т. к. .

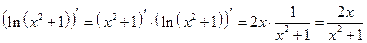Окончательно имеем:

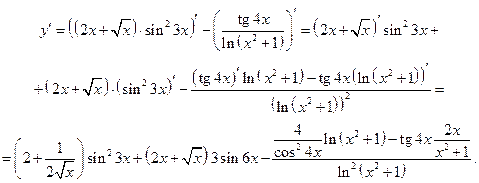
Пример 12.6. Найти производную функции .

Решение. Главное действие – произведение, первый сомножитель – сложная функция.

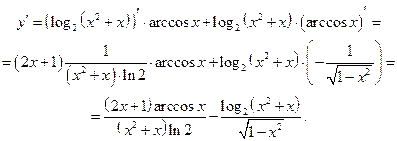
Пример 12.7. ,

Решение. Здесь вначале функция ln, потом действие (сумма), затем сложная функция для второго слагаемого:

Вот так средневековый принцип «разделяй и властвуй» действует в высшей математике.

12.3. Дифференциал сложной функции.
Инвариантность формы дифференциала.

Пусть 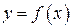, тогда по определению дифференциала 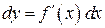. Покажем, что эта форма сохранятся и в том случае, когда 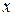является не независимой переменной, а функцией от другого аргумента : .

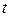Тогда – сложная функция.

По правилу дифференцирования сложной функции , отсюда , т.к. .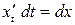

Мы доказали следующую теорему:

Теорема 12.2. Дифференциал сложной функции , для которой 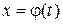, имеет такой же вид , как и в том случае, когда аргумент 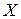является независимой переменной.

Это свойство называется инвариантностью (неизменностью) формы дифференциала.

Пример 12.8. Найти для функции .

Решение. .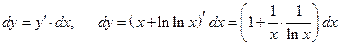

12.4. Производная неявной функции.

Определение 12.3. Уравнение вида 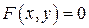, у которой переменная y является функцией от независимой переменной 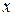, называется неявной.

Примеры неявных функций:

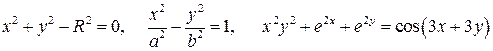Если первые две можно разрешить относительно , то последнюю нельзя, поэтому не будем изобретать приемов для того, чтобы сделать функцию явной, а сразу запишем правило для нахождения производной .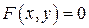

Правило. Для того, чтобы найти для функции 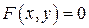необходимо продифференцировать как сложную функцию, считая, что и . Получившееся уравнение разрешить относительно , для чего все члены, содержащие 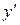оставляют в левой части, остальные переносят в правую часть и выделяют явно . Это выражение и будет искомой производной .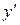

Пример 12.9. Найти , если .

Решение. Для удобства решения первого примера распишем цепочку сложности для :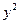

Итак, следуя правилу, берем производную от левой и правой части:

Пример 12.10. Найти , если .

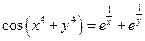Решение. .

Раскроим скобки и члены, содержащие 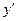перенесем в левую часть, остальные оставим в правой.

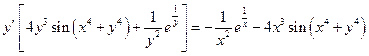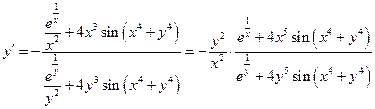Пример 12.11. Найти , если .

Решение. ,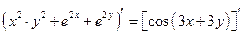

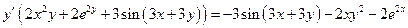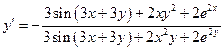То есть можно сказать, что при дифференцировании неявной функции используют прием дифференцирования сложной функции, где при взятии производной учитывается, что 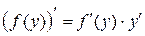. Остальное – дело техники и аккуратного проведения выкладок.

12.5. Дифференцирование показательно-степенной функции.

Определение 12.4. Функция вида называется показательно-степеннойфункцией.

Примеры таких функций:

, , .

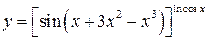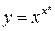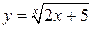Нахождение производной подобных функций производится с помощью предварительного логарифмирования левой и правой части, поэтому дифференцирование степенно-показательных функций называют еще логарифмическим дифференцированием.

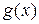Итак, пусть и дифференцируемы в точке 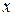, причем 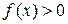. Прологарифмируем выражение 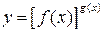по основанию получим:

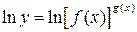
По свойствам логарифма имеем

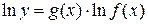– а это неявная функция, брать производную которой мы уже умеем.

откуда

Запоминать эту формулу не надо, проще выполнять все операции каждый раз. Иногда одного логарифмирования недостаточно и следует производить его столько раз, чтобы функции от 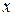не было в показатели степени.

Пример 12.12. Найти 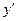, если .

Решение. Логарифмируем левую и правую часть, получаем:

1. – произведение логарифмов,

2. 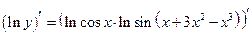– берем производную от левой и правой части равенства

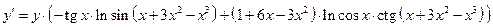3. , где A – множитель при y.

Пример 12.13. ,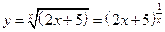

Решение. ,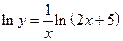

, ,

Пример 12.14. ,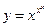

Решение. 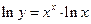. Прологарифмируем это выражение еще раз, т. к. переменная 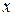осталась в показателе степени.

, , , ,

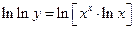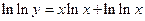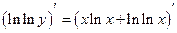12.6. Дифференцирование функций, заданных параметрически

Определение 12.5. Пусть даны две функции переменной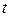

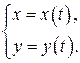(12.3)

рассматриваемые для одних и тех же значений 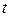. Тогда любому из этих значений 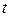соответствуют определенные значения и и, следовательно, определенная точка .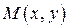

Когда 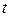пробегает значения из области определения функции (12.3) – точка 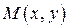описывает некоторую кривую, лежащую в плоскости .

Уравнения (12.3) называются параметрическими уравнениями этой кривой, а переменная 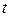– параметром.

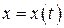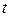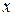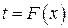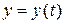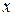Если из уравнения выразить через – получим новую функцию . Подставим ее во второе уравнение , получим , т.е. напрямую зависит от . Эта операция называется исключением параметра.

Роль параметра, в зависимости от задачи, может играть время t или центральный угол j, и чаще всего его исключение не только не обязательно, но и не желательно. Просто надо научиться работать с ними и все.

Например, параметрическими уравнениями окружности в полярной системе координат служат уравнения:

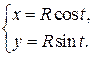, где 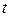– полярный угол.

Уравнение эллипса 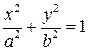в параметрическом виде будет иметь виде:

и т.д.

Итак, если функция от 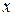задана параметрическими уравнениями (12.2), причем в некоторой области изменения параметра 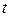функции и дифференцируемы и 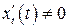, то производная найдется по формуле:

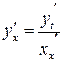. (12.4)

Пример 12.15. Пусть Найти .

Решение. По формуле (12.3) имеем:

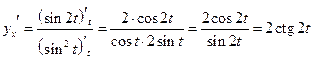Пример 12.16. Найти для функции, заданной параметрически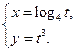

Решение. .

На этом мы заканчиваем обзор различных функций и приемов их дифференцирования.

Для успешного их применения необходимо научиться распознавать функции по способу задания – сложная, параметрическая или иная – т. е. «узнавать их в лицо». А затем применять соответствующие правила и теоремы для их дифференцирования. Здесь нет творчества, есть строгое выполнение инструкций. Этому тоже нужно учиться.

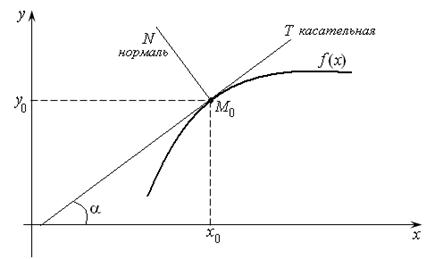
12.7. Уравнение касательной и нормали к кривой в заданной точке

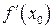Пусть – касательная к графику функции (рис.12.1). Угловой коэффициент равен производной , и все уравнение касательной запишется в виде:

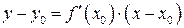. (12.5)

Нормалью к кривой в точке называется прямая, проходящая через точку касания перпендикулярно касательной. Условие перпендикулярности двух прямых дано в теме «Аналитическая геометрия на плоскости» (см. лекцию 7) и выглядит так: 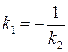. Для нашего случая угловой коэффициент нормали равен , и все уравнение запишется в виде:

. (12.6)