Ранг матриці
Розглянемо матрицю  розмірів
розмірів 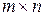 :
:
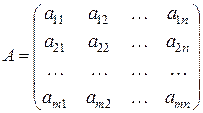 .
.
Виділимо в ній 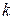 рядків і
рядків і 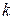 стовпців
стовпців  . З елементів, що стоять на перетині виділених рядків і стовпців, складемо визначник
. З елементів, що стоять на перетині виділених рядків і стовпців, складемо визначник 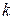 -го порядку. Всі такі визначники називаються мінорами даної матриці. (Відмітимо, що таких мінорів можна скласти
-го порядку. Всі такі визначники називаються мінорами даної матриці. (Відмітимо, що таких мінорів можна скласти 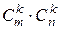 штук, де
штук, де 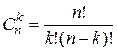 – число сполучень з
– число сполучень з  елементів по
елементів по 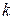 ).
).
Найбільший з порядків мінорів даної матриці, відмінних від нуля, називають рангом матриці і позначають 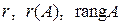 .
.
Очевидно, що  .
.
Мінор, порядок якого визначає ранг, називається базисним. Позначатимемо його 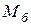 . У ненульової матриці може бути декілька базисних мінорів.
. У ненульової матриці може бути декілька базисних мінорів.
Приклад 3.2.Використовуючи означення, знайти ранг матриці
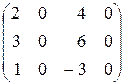
і вказати базисні мінори.
Розв’язок. Серед мінорів 1-го порядку (елементів матриці ) є відмінні від нуля, отже, 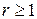 . Серед мінорів 2-го порядку є відмінні від нуля, наприклад:
. Серед мінорів 2-го порядку є відмінні від нуля, наприклад:
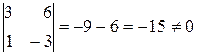 .
.
Отже, 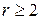 . Всі мінори 3-го порядку рівні нулю. Таким чином,
. Всі мінори 3-го порядку рівні нулю. Таким чином, 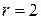 .
.
В якості базисного мінору можна взяти
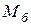 =
= або
або 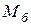 =
=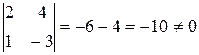 . t
. t
Відмітимо властивості рангу матриці:
1. При транспонуванні матриці її ранг не змінюється.
2. Якщо викреслити з матриці нульовий рядок або стовпчик, то її ранг не зміниться.
3. Ранг матриці не змінюється при елементарних перетвореннях матриці.
Неважко показати, що за допомогою елементарних перетворень будь-яку ненульову матрицю  можна привести до трапецієвидного вигляду:
можна привести до трапецієвидного вигляду:
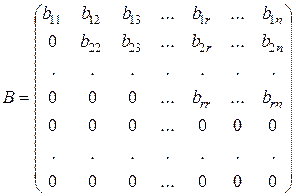 ,
,
де 
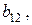 …,
…,  відмінні від нуля.
відмінні від нуля.
Викреслимо в матриці В рядки, всі елементи яких рівні нулю. Ранг отриманої матриці, що складається з  рядків, рівний
рядків, рівний  , так як мінор порядку
, так як мінор порядку  , що стоїть у верхньому лівому куті, відмінний від нуля. Отже, і ранг матриці В рівний
, що стоїть у верхньому лівому куті, відмінний від нуля. Отже, і ранг матриці В рівний  – кількості ненульових рядків.
– кількості ненульових рядків.
Так як матриця В отримана з матриці А шляхом елементарних перетворень, то ранг матриці А теж рівний  .
.
Приклад 3.3.Знайти ранг матриці
 .
.
Розв’язок. За допомогою елементарних перетворень зведемо дану матрицю до трапецієвидного вигляду:
 .
.
Ранг отриманої матриці рівний трьом, а отже і ранг даної матриці рівний трьом. t
Теоретичні питання
3.1. Яка матриця називається невиродженою?
3.2. Яка матриця називається союзною?
3.3. Яка матриця називається оберненою?
3.4. Для якої матриці існує обернена?
3.5. Запишіть формулу, за якою знаходиться обернена матриця.
3.6. Які властивості оберненої матриці?
3.7. Що називається мінором матриці?
3.8. Що називається рангом матриці?
3.9. Що називається базисним мінором матриці?
3.10. Як знайти ранг матриці за допомогою елементарних перетворень?
Задачі та вправи
3.1. Знайти матриці, обернені до даних, якщо вони існують:
а)  ; б)
; б)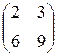 ; в)
; в) 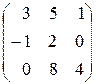 ; г)
; г)  .
.
3.2. Знайти ранг матриці та вказати один із базисних мінорів:
а) 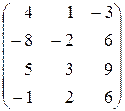 ; б)
; б)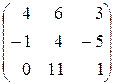 ; в)
; в) 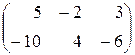 .
.