Тема 6. Средние величины
6.1. Сущность и значение средней величины.
Виды средних величин.
6.2. Среднее значение признака, методы его расчета.
6.3. Структурные средние величины.
6.1. Сущность и значение средней величины.
Виды средних величин
Средняя величина – один из самых распространенных приемов обобщений, в которых находят выражение действие общих условий, закономерность развития изучаемого явления. Средняя величина позволяет через единичное и случайное выявить общее в развитии общественного явления.
Средняя величина – это наиболее обобщенная характеристика совокупности по количественно-варьирующему признаку в расчете на единицу однородной совокупности.
Правило: средние величины должны исчисляться на основе массового обобщения фактов и применяться к качественно однородным совокупностям.
Средняя величина отражает то общее, типичное, что складывается в отдельном изучаемом явлении, поэтому она должна дополняться другими аналитическими показателями, так как за общими благополучными средними могут скрываться серьезные недостатки.
Каждая средняя величина характеризует совокупность только по какому-либо одному признаку. Чтобы получить полное представление об изучаемом явлении (совокупности по ряду признаков), надо рассчитать систему средних величин.
Средние величины измеряются в тех же единицах, что и признак.
В статистике выделяют следующие виды средних величин:
ü среднее значение признака,
ü структурные средние величины (мода, медиана).
6.2. Среднее значение признака,
методы его расчета
Для расчета среднего значения признака в статистике применяются следующие методы расчета средних величин:
ü средняя арифметическая,
ü средняя гармоническая,
ü средняя квадратическая (применяется при исчислении показателей вариации),
ü средняя хронологическая (применяется для расчета среднего уровня ряда в моментных статистических рядах динамики с равными периодами времени между наблюдениями),
ü средняя геометрическая (применяется при исчислении средних темпов роста в статистических рядах динамики).
Средняя арифметическая – отношение объема варьирующего признака к числу единиц совокупности:
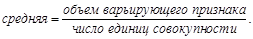(1)
Используется две ее формы:
ü простая – когда объем варьирующего признака рассчитывается как сумма значений признака каждой единицы совокупности:
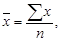(2)
где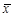 
– среднее значение признака, å – знак суммы «сигма», x – значение признака (варианта), åx – объем варьирующего признака, n – число единиц совокупности.
Средняя арифметическая простая применяется в случаях, когда имеются значения признака по каждой единице совокупности, т. е. на индивидуальных данных.
ü взвешенная – когда объем варьирующего признака рассчитывается как сумма произведений значений признака на частоту (вес) (f), а число единиц совокупности (n) рассчитывается как сумма частот (n = åf):
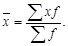(3)
Средняя арифметическая взвешенная применяется в случаях, когда имеются значения признака (x) – качественная особенность единицы совокупности и частота (вес) (f) – число единиц совокупности, обладающих данным значением признака. Указанные характеристики выступают элементами статистического ряда распределения, а так как средняя величина – это наиболее обобщенная характеристика совокупности по количественно-варьирующему признаку, то – вариационного статистического ряда распределения.
Таким образом, сфера применения средней арифметической взвешенной – вариационные статистические ряды распределения, которые делятся на два вида:
1. Дискретные – если значения признака представлены отдельными (дискретными) числами. Тогда среднее значение признака рассчитывается непосредственно по формуле средней арифметической взвешенной;
2. Интервальные – если значения признака представлены диапазонами, интервалами. Тогда для применения формулы средней арифметической взвешенной необходимо значения признака представить в виде дискретных чисел, т. е. перейти от интервального вариационного статистического ряда распределения к дискретному. Для этого по каждому интервалу значений признака рассчитывается среднее значение признака (как наиболее обобщенная характеристика совокупности по количественно-варьирующему признаку) по формуле средней арифметической простой:
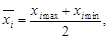(4)
где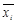 
– среднее значение признака в i-ом интервале, xi max – верхняя граница i-го интервала, xi min – нижняя граница i-го интервала.
При этом открытые интервалы (т. е. описанные только одной границей – верхней или нижней) закрывают по правилу:
– первый закрывают по длине второго,
– последний – по длине предпоследнего.
Свойства средней арифметической:
ü произведение среднего значения признака на число единиц совокупности равно объему варьирующего признака:
(5)
или
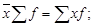(6)
ü сумма отклонений значений признака от среднего значения признака равна нулю:
(7)
или
(8)
ü если все частоты разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится:
(9)
Средняя гармоническая (как частный случай средней арифметической) – используется в случаях, если известны значения варьирующего признака, и объем варьирующего признака (произведение признака на частоту – х·f), но нет информации о числе единиц совокупности. В практике чаще всего применяется в форме взвешенной:
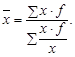(10)
Средняя квадратическая – корень квадратный из среднего квадрата значений признака (применяется как показатель вариации признака):
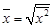(11)
– в форме простой, если средний квадрат значений признака рассчитывался по формуле средней арифметической простой, т. е. на индивидуальных данных:
(12)
и тогда
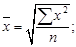(13)
– в форме взвешенной, если средний квадрат значений признака рассчитывался по формуле средней арифметической взвешенной:
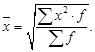(14)
Cредняя хронологическая – как отношение суммы половины первого и последнего значений признака и полных промежуточных значений признака к числу единиц совокупности, уменьшенному на единицу:
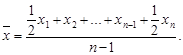(15)
Средняя геометрическая – корень n-й степени из произведения (П) значений признака (х1,х2,…,xn):
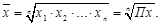(16)