Расчет средних показателей анализа статистического ряда динамики.

Средний абсолютный прирост – как средняя арифметическая простая цепных абсолютных приростов:

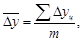(15)

где m – число цепных абсолютных приростов.

При этом, так как сумма абсолютных приростов цепных равна абсолютному приросту базисному для последнего периода наблюдения, т. е.

ΣΔy_ц = Δy_ц2 + Δy_ц3 + … + Δy_цn = (y₂ – y₁) + (y₃ – y₂) + …

+ (y_n-1 – y_n) = y_n – y₁ = Δy_бn, (16)

а число цепных абсолютных приростов на 1 меньше, чем периодов наблюдения, т. е.

m = n – 1, (17)

то

(18)

Средний коэффициент роста – по формуле средней геометрической цепных коэффициентов роста:

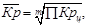(19)

где m – число цепных коэффициентов роста, Π – знак произведения.

При этом, так как произведение коэффициентов роста цепных равно коэффициенту роста базисному для последнего периода наблюдения, т. е.

(20)

а число цепных коэффициентов роста на 1 меньше, чем периодов наблюдения, т. е.

m = n – 1, (21)

то

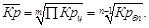(22)

Средний темп роста – как средний коэффициент роста, выраженный в процентах:

(23)

Средний темп прироста определяется исходя из взаимосвязи между темпом роста и темпом прироста (12):

(24)

 

2. Аналитическое выравнивание статистического ряда динамики по математической кривой (прямой, параболе, гиперболе и т. д.) позволяет найти плавную линию развития (тренд) данного явления.

Сущность метода аналитического выравнивания заключается в том, чтобы представить тренд как временнэю функцию:

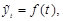(25)

где – уровни тренда, t – время.

Аналитическое выравнивание по прямой линии производят, если явление во времени развивается равномерно, когда развитие равноускоренное (равнозамедленное), т. е. стабильны абсолютные приросты, коэффициенты (темпы) роста, темпы прироста. При переменном развитии явления (ускорение, потом замедление или наоборот) выравнивание производится по формулам кривых линий (тема 11, п. 11.3). В целом выбор временной функции определяется темпами развития явления во времени.

Простейшим способом аналитического выравнивания выступает выравнивание по функции прямой линии:

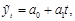(26)

где – параметры уравнения: a₀, – свободный член уравнения, характеризующий обобщающее влияние на результат всех факторов, кроме рассматриваемого (времени), a₁ – коэффициент регрессии, измеряющий среднее отклонение результативного признака (уровня ряда, y) от его средней величины при отклонении факторного признака (времени, t) на одну единицу его измерения – вариация y, приходящаяся на единицу вариации t.

Кроме того, указывает направление развития явления:

при 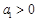– рост уровней ряда в среднем на эту величину (равномерный),

при – снижение уровней ряда в среднем на эту величину (равномерное).

Нахождение параметров уравнения осуществляется методом наименьших квадратов через систему нормальных уравнений:

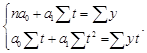(27)

Для упрощения техники расчета в рядах динамики показателям времени (t) придают такие значения, чтобы их сумма была равна нулю, т. е. Σt = 0. В рядах динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначается как ноль (условное начало отсчёта времени, «0»), показатели времени всех предыдущих уровней обозначаются с интервалом (-1), а всех последующих – с интервалом (+1) (например, при n = 5 t будут: -2, -1, 0, +1, +2). При чётном числе уровней (например, n = 6) условный шаг будет равен двум, т. е. порядковые номера левой по­ловины ряда (от середины ранние периоды) обозначатся числами (от меньшего к большему): -5, -3, -1, а правой половины (от середины поздние периоды): +1, +3, +5.

Тогда уравнения примут следующий вид:

(28)

откуда

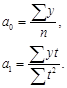(29)

Определив параметры а₀ и а₁, можно вычислить теоретические уровни, т. е. ординаты точек искомой прямой.