Средние величины.

Средняя величина представляет собой обобщенную характеристику совокупности однородных явлений по какому-либо одному количественно варьируемому признаку.

Средние величины играют важную роль, в статистике. С их помощью можно сравнивать различные совокупности значимых явлений по некоторому количественному признаку и делать из этого сравнения необходимые выводы. Одно из важнейших условий расчета средних величин – это качественная однородность единиц совокупности в отношении осредняемого признака.

На практике чаше всего применяют групповые средние, то есть средние, рассчитанные на основе статистических группировок. Средние величины основываются на массовом обобщении фактов. Только при этом условии они способны обнаружить те или иные тенденции изучаемых явлений и процессов. Вычисление средних величин производится, на основе вариационных рядов.

Различают несколько видов средних величин: среднюю квадратическую, среднюю арифметическую, среднюю геометрическую, среднюю гармоническую, среднюю хронологическую. Исчисляются как простые, так и взвешенные средние. Формулы средних (кроме хронологической) получаются из общей формулы степенной средней.

Пусть имеем некоторый количественный показатель X. В результате наблюдения зафиксированы следующие его значения (варианты): х₁, х₂, …, х_n.

Общая формула степенной средней имеет вид:

где m – целое число.

Если среди наблюдаемых значений х₁, х₂, …, х_n встречаются одинаковые, то приведенную выше формулу можно записать несколько иначе.

Пусть значение х₁ наблюдалось n₁ раз, х₂ n₂ раз, ... , х_k – n_k раз._. При этом, очевидно, n₁ + п₂ + ...+ п_к = n_. Тогда общая формула степенной средней может быть записала так: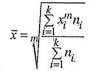

 

Частоты n_i называют еще весами средней, а сама эта средняя называется взвешенной степенней средней.

Простая, и взвешенная средние по сути определяются по одной и той же формуле. Только для взвешенной средней суммирование одинаковых по значению величин заменяется умножением значения величины на число раз сколько она встречалась.

Если m=2, то получаем среднюю квадратическую; если m= 1, то приходим к средней арифметической; при m=0 получаем среднюю геометрическую; при т=-1 имеем среднюю гармоническую.

Заметим, что все формулы степенных средних, за исключением средней геометрической, легко получаются из общей формулы степенной средней.

Для ввода формулы средней геометрической следует вычислить предел:

Его несложно найти, проведя логарифмирование и используя правило Лопиталя.

Чем меньше значение т, тем меньше величина соответствующей средней при одних и тех же значениях х₁, х₂, …, х_n. Это свойство мажорантности средних:

Выбор вида средней определяется путем конкретного анализа изучаемой совокупности, исходя из принципа осмысленности результатов при суммировании и при взвешивании. Только тогда средняя применена правильно, когда она имеет реальный смысл.

В статистике самое широкое применение находит средняя арифметическая.

Средняя геометрическая используется при вычислений среднегодовых темпов прироста исследуемых показателей.

Средняя квадратическая играет важную роль при изменении связей между изучаемыми явлениями и их причинами.

Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине заданного признака, то есть когда суммированию подлежат не сами варианты, а обратные им величины.

В тех случаях, когда значения показателя x_i известны в конкретные моменты времени t_i, используют среднюю хронологическую.

В табл. 1.2 приведены формулы различных видов средних величин.

Кроме средних, приведенных выше, для характеристики среднего значения варианты в вариационном ряду могут быть взяты не расчетные, а описательные средние: мода и медиана.

Мода (Мо) - наиболее часто встречающаяся варианта в вариационном ряду, то есть варианта, которой соответствует наибольшая частота.

Медиана (Me) - значение варианты, находящейся в середине вариационного ряда.

Таблица 1.1.

Формулы для различных видов средних величин

 

№ п/п	Наименование средней	Формулы средних
простой	взвешенной
1.	Средняя арифметическая
2.	Средняя геометрическая
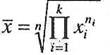
3.	Средняя гармоническая
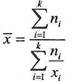
4.	Средняя квадратическая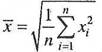
5.	Средняя хронологическая

 

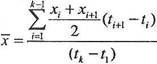
Определение моды и медианы в случае интервальных рядов распределения несколько сложнее.

В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Поэтому в модальном интервале необходимо определить модальную варианту. При этом надо иметь в виду, что при расчетах будет получено не точное, а некоторое условное значение моды, так как неизвестен характер распределения частоты внутри модального интервала.

Вычисление моды производится по следующей формуле:

 

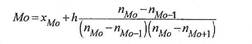
где x_Mo – начало (нижняя граница) модального интервала;

h – величина интервала;

n_Mo – частота модального интервала;

n_Mo-1 – частота интервала, предшествующего модальному;

n_Mo+1 – частота интервала, следующего за модальным.

Расчет медианы для интервального ряда производится по формуле:

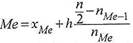
где x_Mе – начало (нижняя граница) медианного интервала;

h – величина интервала;

n_Mе – частота медианного интервала;

n_Mе-1 – накопленная частота вариант, предшествующих медианному интервалу;

n – сумма частот всех вариант в вариационном ряду.

Мода и медиана характеризуют структуру распределения, поэтому их называют структурными позиционными средними.