Плотность вероятностей

Разобьём всю ширину ранжированной выборки на несколько интервалов одинаковой ширины Δx и определим количество наблюдений m_i, попавших в каждый из интервалов. Затем для каждого интервала вычислим функцию:

(1/час)

где Δx –ширина интервала; i – номер интервала;

m_{i –} количество наблюдений, попавших в интервал;

N – общее количество наблюдений в выборке.

Эта функция называется эмпирической (опытной) плотностью вероятностей.

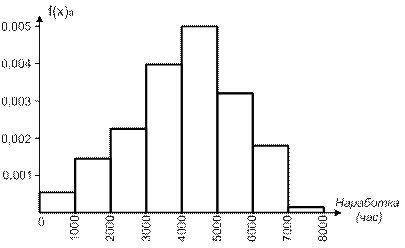
График этой функции (ступенчатая диаграмма) называется гистограммой плотности вероятностей.

Высота каждого столбца гистограммы характеризует частоту отказов, среднюю для данного интервала. Например, если для четвёртого интервала (от 3000 до 4000 часов) f(x)_э = 0,004, это означает, что в данном интервале наблюдений следует ожидать в среднем четыре отказа на каждую тысячу часов работы этого вида оборудования.

Если эмпирическую плотность вероятностей умножить на ширину интервала, то полученное произведение будет равно отношению числа наблюдений, попавших в данный интервал, к общему количеству наблюдений в выборке. Это отношение характеризует вероятность того, что отказ оборудования произойдет именно в данном периоде его эксплуатации:

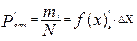
Если обратиться к графику, то нетрудно увидеть, что произведение высоты столбца на его ширину представляет собой площадь этого столбца.

Таким образом, площадь каждого столбца гистограммы численно равна вероятности того, что отказ оборудования произойдет в данном временном интервале работы оборудования.

Следует отметить, что применение эмпирической плотности вероятностей даёт возможность довольно приблизительной оценки вероятностей отказов, поскольку границы интервалов заранее заданы и внутри каждого интервала частота отказов считается величиной постоянной. Для более точного решения следует применять теоретическую плотность вероятностей.

Для получения этой функции будем в эмпирической плотности вероятностей сокращать ширину интервалов, соответственно увеличивая их количество. При этом гистограмма будет постепенно сглаживаться.

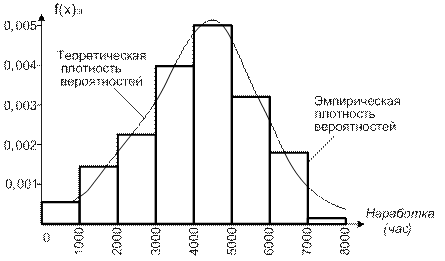
В пределе, когда ширина интервалов станет бесконечно малой величиной, эмпирическая плотность вероятностей превратится в непрерывную гладкую функцию, которую называют теоретической плотностью вероятностей:

f(x)_т = f(x)_эприΔx→ 0

С помощью теоретической плотности вероятностей для любого заданного момента эксплуатации tможно определить ожидаемую частоту отказов f(t)оборудования (см. приведенный ниже рисунок).

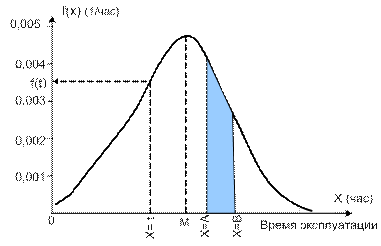
Для определения вероятности отказа оборудования на интервале конечной ширины (на рисунке от Х=А до Х=B) необходимо проинтегрировать теоретическую плотность вероятностей на этом интервале:

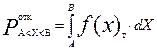
Этот приём может быть использован, например, для оценки вероятности отказа оборудования во время рейса, если задана плотность вероятностей отказов данного типа оборудования и известны время начала и окончания рейса (А и В на рисунке).

Теоретическая плотность вероятностей является дифференциальной формой закона распределения случайной величины. На практике применяют несколько типовых форм законов распределения.

Для нормального закона распределения теоретическая плотность вероятностей аналитически описывается кривой Гаусса. Её графическое изображение имеет вид, показанный на приведенных выше рисунках. Значение Х, соответствующее максимуму этой функции, называется математическим ожиданием. Оно соответствует наиболее вероятному сроку эксплуатации оборудования до отказа.

При оценке показателей надежности применяют и другие типовые законы: экспоненциальный, равномерный, Вейбулла и другие. Второй символ пароля теста «7».