Корреляционный анализ

Допустим, что накопленные статистические данные представляют собой массив не одиночных, а парных наблюдений:

Параметр Х	X₁	X₂	. . .	X_i	. . .	X_N
Параметр Y	Y₁	Y₂	. . .	Y_i	. . .	Y_N

При этом возникают 3 вопроса:

· имеется ли какая-то функциональная взаимосвязь параметров X и Y?

· если да, то каким видом функции она может быть выражена?

· какие численные значения должны быть у коэффициентов этой функции?

На первый и второй вопросы можно ответить с помощью корреляционного анализа, на второй и третий – с помощью регрессионного анализа.

Корреляционный анализ называют парным, если сопоставляются два ряда наблюдений, и множественным, если число параметров больше двух. Мы ограничимся рассмотрением парного анализа.

Первым этапом парного корреляционного анализа обычно является попытка установить наличие линейной взаимосвязи параметров. Для этого вычисляют коэффициент линейной корреляции по формуле:

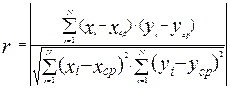
Диапазон изменения коэффициента линейной корреляции: 0 ≤ r ≤ 1. Чем больше величина коэффициента, тем ближе функциональная взаимосвязь параметров к линейной.

На приведённых графиках точки соответствуют заданным сочетаниям значений параметров X и Y, а прямые линии отображают возможную линейную взаимосвязь параметров:

Каким образом можно однозначно ответить на вопрос: можно считать связь параметров линейной, или нельзя?

Строгий анализ можно выполнить путём оценки значимости коэффициента линейной корреляции с помощью критерия Стьюдента. На практике часто используют упрощённый метод оценки: если r ≥ 0,8 - можно считать, что между параметрами X и Y имеется линейная зависимость, конкретные коэффициенты которой можно определить с помощью регрессионного анализа.

Что делать, если оказалось, что линейной функцией нельзя корректно описать взаимосвязь параметров X и Y? В этом случае можно использовать метод преобразования параметров для поиска другого вида функциональной зависимости.

Например, можно ввести функции U = k₁lnX V = k₂·sinY и провести парные корреляционные анализы по приведённой ниже схеме:

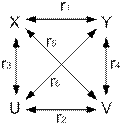
Если в результате получилось, что самый большим и значимым оказался, например, коэффициент r₅, это означает, что функциональная взаимосвязь параметров может иметь следующий вид: X = k₂sinY

Вариантов таких дополнительных функционалов может быть огромное множество, поэтому такой поиск может быть выполнен только с помощью специальных компьютерных программ.