Метод Гаусса-Зайделя
Суть метода заключается в последовательном движении к оптимуму путем поочередного изменения варьируемых факторов.
План эксперимента представляет собой ряд серий опытов, причем внутри каждой серии изменяется только один из факторов, (то есть каждая серия представляет собой однофакторный эксперимент). Серия продолжается до тех пор, пока опыты приводят к улучшению результата. Если результат начинает ухудшаться, тот опыт, в котором получен наилучший для данной серии результат, выбирается в качестве отправной точки для планирования следующей серии опытов, во время которой изменяется другой фактор, и т. д.
Поясним суть метода на простейшем примере, когда число варьируемых параметров (факторов) равно 2 (это условие обеспечивает наиболее наглядную графическую иллюстрацию).
Пусть свойства объекта описываются математической моделью-функцией цели: Y = f(X1, X2), где:
Y - критерий оптимизации, Х1, Х2 - варьируемые факторы.
Графическая интерпретация модели объекта может быть представлена семейством замкнутых кривых, соответствующих фиксированным значениям критерия оптимизации (линий равного уровня).
Задачей эксперимента является нахождение координат "вершины", т.е. сочетания численных значений факторов X1 и Х2, при котором критерий оптимизации имеет максимальное значение (разумеется, решая эту задачу, экспериментатор не располагает априорной информацией о свойствах объекта, представленной на рисунке).
Начиная движение к оптимуму от исходной точки 0 с координатами: Х1(о), X2(0), экспериментатор выбирает индекс варьируемого фактора, шаг его варьирования и направление движения.
Если в качестве первого варьируемого фактора выбран, например, Х2, план первой серии опытов описывается условием: X1 = X1(0) = idem; Х2 = var, причем изменения фактора X2 от опыта к опыту производятся с заданным шагом ΔX2
Сравнивая результат первого опыта Y(1) с исходным значением критерия Y(0), экспериментатор судит о правильности выбранного направления: если Y(1) хуже, чем Y(0) - следует поменять знак ΔХ2 на противоположный.
Серия продолжается до тех пор, пока продолжается улучшение результата. Как только результат начинает ухудшаться, экспериментатор принимает решение об остановке данной серии опытов и переходит к следующей серии, в которой изменяется уже другой фактор.
В качестве начальной точки движения для второй серии выбирается опыт, давший в первой серии наилучший результат (в примере, показанном на рисунке, это опыт № 3)
Условия проведения второй серии опытов:
Х2 = Х2(3) = idem, X1 = var, причём изменения фактора X1 от опыта к опыту производятся с заданным шагом ΔX1 .
Продолжая действовать в соответствии с описанным алгоритмом, экспериментатор от опыта к опыту последовательно улучшает выбранный критерий оптимизации (что является достоинством метода).
Кроме того, уменьшая шаги изменения факторов, можно сколь угодно близко подойти к оптимальной точке (при отсутствии ограничений по числу опытов), т.е. решить оптимизационную задачу с любой заданной точностью (второе достоинство метода).
Недостатком является сравнительно медленное движение к оптимуму, что может приводить к неоправданному увеличению числа опытов, особенно при увеличении числа варьируемых факторов, и, как следствие, к снижению технико-экономических показателей эксперимента.
3.3.4 Метод Бокса-Уилсона (градиентный метод)
Идея метода заключается в том, что, с целью наискорейшего достижения оптимума, направление движения к нему выбирается совпадающим с направлением градиента функции цели в окрестности отправной точки. Направление градиента функции определяет направление наиболее интенсивного изменения функции, т.е. наибольшей крутизны, поэтому градиентный метод называют также методом крутого восхождения (при движении к максимуму) или методом наискорейшего спуска (при движении к минимуму).
Поскольку это направление априорно неизвестно, необходимо предварительно исследовать окрестность отправной точки, спланировав вокруг неё, как вокруг центра, двухуровневый полный или дробный факторный эксперимент.
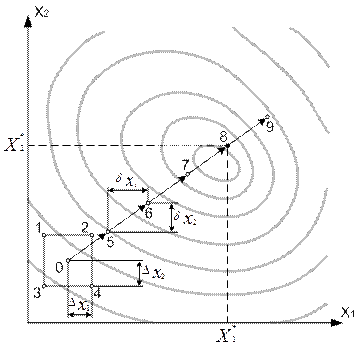
Для рассматриваемого простого двухфакторного примера эта предварительная серия должна включать 4 опыта, условия которых определяются сочетаниями нижних и верхних уровней факторов.
- верхние уровни: X1в = X1(0) + ΔX1 X2в = X2(0) + ΔX2
- нижние уровни: X1н = X1(0) - ΔX1 X2н = X2(0) - ΔX2
где ΔX1 и ΔX2 - назначенные экспериментатором интервалы варьирования.
На рисунке, условия опытов определяются координатами вершин прямоугольника 1– 2 – 3 – 4.
Условия проведения опытов и их результаты заносят в таблицу, которая называется матрицей планирования:
| № опыта | Факторы | Результаты опытов | |||
| X1 | X2 | ||||
| Истинное значение | Относит. значение | Истинное значение | Относит. значение | ||
| Х1(1) | -1 | Х2(1) | -1 | У(1) | |
| Х1(2) | -1 | Х2(2) | +1 | У(2) | |
| Х1(3) | +1 | Х2(3) | +1 | У(3) | |
| Х1(4) | +1 | Х2(4) | -1 | У(4) |
После заполнения матрицы вычисляют коэффициенты
регрессии: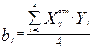 
где: i – номер опыта; j – индекс фактора и соответствующего коэффициента.
Затем один из факторов назначают базовым, например X1 , и выбирают шаг движения к оптимуму для базового фактора δX1 = δБАЗ
Для остальных факторов (в данном примере это фактор X2) шаг движения к оптимуму определяют по формуле: 
После этого начинают движение к оптимуму, задавая приращения факторам в соответствии с определенными шагами δj , а именно:
- опыт 5: X1(5) = X1(0) + δX1 X2(5) = X2(0) + δX2
- опыт 6: X1(6) = X1(5) + δX1 X2(6) = X2(5) + δX2 и т.д.
Действия в соответствие с рассмотренным алгоритмом обеспечат движение к оптимуму в направлении градиента целевой функции, определённого для окрестности начальной точки 0.
Движение к оптимуму продолжается до тех пор, пока наблюдается улучшение результата. При нарушении этого условия эксперимент прекращается и оптимальным сочетанием значений факторов считаются условия опыта, давшего наилучший результат (на рисунке это опыт 8).
Преимуществом данного метода является быстрое движение к оптимуму.
Недостатки:
- зависимость конечного результата от точности проведения опытов в предварительной серии (погрешности искажают оценку направления градиента);
- зависимость конечного результата от свойств объекта (направление градиента в окрестности начальной точки может существенно отличаться от направления на "вершину").
Избежать указанных недостатков (пожертвовав в определенной степени и преимуществом) удается применением безградиентных многофакторных методов экспериментальной оптимизации, например, последовательного симплексного метода планирования эксперимента.
3.3.5 Последовательный симплексный метод
В этом методе условия опытов определяются в факторном пространстве координатами вершин симплексов (обычно применяют правильные симплексы).
Правильным симплексом называется правильный выпуклый многогранник, имеющий К+1 вершину в К-мерном факторном пространстве.
Для К=2 факторное пространство - плоскость, правильный симплекс -равносторонний треугольник.
Для К=3 в трёхмерном факторном пространстве правильным симплексом является тетраэдр.
Для К>3 симплекс представляет собой гипертетраэдр в К-мерном гиперпространстве.
Поиск оптимума симплексным методом начинается с построения начального симплекса в окрестности начальной точки. При этом размер симплекса выбирают, руководясь следующими соображениями:
слишком большая величина ребра симплекса приведёт к грубому решению задачи, слишком мелкий симплекс потребует выполнения большого количества опытов.
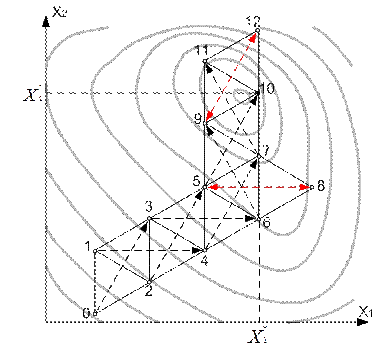
Ориентация начального симплекса в факторном пространстве в общем случае произвольна, однако для упрощения построений и вычислений рекомендуется одну из сторон симплекса ориентировать параллельно одной из координатных осей факторного пространства.
Проведя опыты в соответствии с координатами вершин начального симплекса, находят вершину, давшую наихудший результат, и строят следующий симплекс путем зеркального отражения этой вершины относительно противоположной грани.
Проведя опыт в соответствии с координатами новой вершины, снова находят вершину, давшую наихудший результат в достроенном симплексе, и продолжают последовательное достраивание симплексов описанным способом, проводя в каждом симплексе, начиная со второго, уже только один опыт.
Некоторые осложнения могут возникнуть, когда симплекс попадёт на гребень поверхности отклика и начнёт колебаться, поскольку отражение вершины, давшей худший результат, приводит к возврату на отражённую вершину предыдущего симплекса.
Для устранения колебаний следует исключить в последнем симплексе вершину с наихудшим результатом (опыт 5 на рисунке) и отражать наихудшую из оставшихся (опыт 6).
Если этот прием не устраняет колебания - делается вывод о достижении области оптимума. Другим признаком близости оптимума является вращение симплекса вокруг одной из вершин (на рисунке вершина 10). В обоих случаях либо останавливают процесс и считают оптимальным сочетанием значений факторов координаты вершины, давшей наилучший результат, либо продолжают поиск в её окрестности, уменьшив размер симплекса с целью уточнения результата.
Нетрудно видеть, что алгоритм достраивания симплексов предусматривает продвижение в факторном пространстве в сторону, противоположную областям, дающим наихудший результат. Благодаря этому реализация ПСМ обеспечивает последовательное улучшение критерия оптимизации.
Другим важным положительным качеством ПСМ является его устойчивость к погрешностям. Это объясняется тем, что допустимые погрешности измерения, как правило, не оказывают влияние на результат качественного анализа при выборе наихудшей вершины симплекса, а грубый промах вызывает временное отклонение поиска, которое затем «автоматически» возвращается к истинному направлению.
Не менее важным преимуществом ПСМ по сравнению с градиентным методом является его адаптивность к свойствам объекта (форме поверхности отклика), обеспечивающая как бы «автоматическую» корректировку направления поиска в процессе эксперимента с гарантированным выходом в зону оптимума.
Недостатком является несколько замедленное по сравнению с градиентным методом продвижение к цели, особенно при неудачном выборе размера симплекса.
В целом, по совокупности достоинств и недостатков можно сказать, что ПСМ занимает промежуточное положение между методом Гаусса-Зайделя и градиентным методом.