Визначення «жорстких» та «м’яких» математичних моделей динаміки популяцій
Розглянемо найпростішу модель динаміки популяції – модель Мальтуса:
 (r=b-d) (12.14)
(r=b-d) (12.14)
Модель Мальтуса передбачає необмежене зростання чисельності популяції по експоненціальному закону, однак в природі необмежене зростання неможливе, так як стримуючі фактори присутні завжди. Отже, модель мальтуса досить «жорстка» і не може описувати зростання чисельності популяції протягом тривалого періоду. «Жорсткість» цієї моделі пов’язана з параметром r, який вважається сталим. Тому «жостку» модель Мальтуса доцільно замінити іншою, так званою «мякою» моделлю:
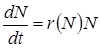 , (12.15)
, (12.15)
де параметр 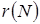 розглядається як змінна величина, що залежить від чисельності популяції і може враховувати зворотний зв’язок, який може набути такого вигляду:
розглядається як змінна величина, що залежить від чисельності популяції і може враховувати зворотний зв’язок, який може набути такого вигляду:
 (12.16)
(12.16)
Внаслідок таких уточнень я заміни постійного («жосткого») параметра r змінним («м’яким»), одержимо так звану логістичну модель Фергюльста , які запишемо у вигляді:
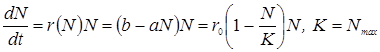 (12.17)
(12.17)
Побудуємо графіки залежності швидкості розмноження популяції від її чисельності та графік чисельності популяції залежно від часу для обох моделей.
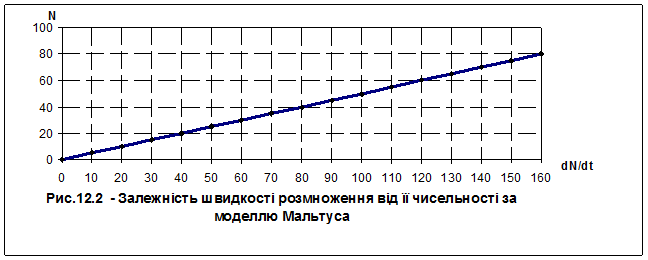
Аналіз рис.12.2 дозволяє зробити висновок, що похідна функції N(t) додатня при t>0. Отже функція N(t) буде зростаючою при всіх N>0 (рис.12.3).


Аналіз рис.12.4 дозволяє зробити висновок, що для логістичної моделі в точках О і К швидкість розмноження популяції дорівнює нулю: це стаціонарні точки. Похідна функції N(t) додатня при  і від’ємна при
і від’ємна при  . Отже функція N(t) буде зростаючою при
. Отже функція N(t) буде зростаючою при  і спадною при
і спадною при  .
.

За рис.12.5 очевидно, що логістична модель прогнозує встановлення з часом стаціонарного режиму N=K, який є стійким, тобто кількість особин, що перевищує К, зменшується, а кількість особин, що менша за К, збільшується.
Примітка: Населення Землі на сьогоднішній день становить близько 6 млрд, стаціонарне значення за різними оцінками всених становить 16-20 млрд осіб.