Продуктивные модели Леонтьева
Матрица  называется продуктивной, если для любого вектора
называется продуктивной, если для любого вектора 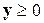 существует решение
существует решение 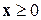 уравнения
уравнения  . Соответственно и модель Леонтьева, определяемая матрицей A, тоже называется продуктивной. Иными словами, модель продуктивна, если можно найти необходимый объем валового выпуска для любого заданного уровня конечного потребления.
. Соответственно и модель Леонтьева, определяемая матрицей A, тоже называется продуктивной. Иными словами, модель продуктивна, если можно найти необходимый объем валового выпуска для любого заданного уровня конечного потребления.
Первый критерий продуктивности. Если  и для некоторого положительного вектора
и для некоторого положительного вектора 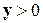 уравнение
уравнение  имеет решение
имеет решение 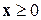 , то матрица A продуктивна.
, то матрица A продуктивна.
Опуская строгое доказательство, заметим, что если возможно выделить некоторую часть от всех производимых видов продукции (все компоненты вектора y предполагаются строго больше нуля) для конечного потребления, то естественно предполагать, что и для любого другого уровня конечного потребления задача разрешима.
Второй критерий продуктивности. Матрица  продуктивна тогда и только тогда, когда существует и неотрицательная матрица
продуктивна тогда и только тогда, когда существует и неотрицательная матрица 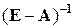 .
.
Докажем достаточность. Если E – единичная матрица, то рассматриваемое уравнение можно записать как 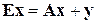 , или
, или 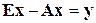 и, наконец
и, наконец 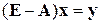 . Поскольку предполагается, что существует матрица, обратная к матрице
. Поскольку предполагается, что существует матрица, обратная к матрице 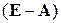 , то можно умножить на нее слева обе части уравнения. Получим
, то можно умножить на нее слева обе части уравнения. Получим 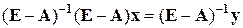 и окончательно:
и окончательно:
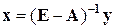 .
.
Следовательно, искомый вектор валового выпуска x существует и при неотрицательной обратной матрице и 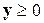 будет также неотрицателен, что и требовалось доказать.
будет также неотрицателен, что и требовалось доказать.
Для доказательства необходимости обозначим столбцы единичной матрицы как 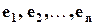 . Так как матрица A предполагается продуктивной, то существуют векторы (столбцы)
. Так как матрица A предполагается продуктивной, то существуют векторы (столбцы) 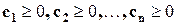 , являющиеся решениями уравнений:
, являющиеся решениями уравнений:
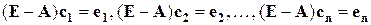 ,
,
которые можно заменить одним уравнением
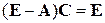 ,
,
если составить матрицу C из столбцов 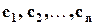 . Следовательно, существует неотрицательная матрица C,обратная к матрице
. Следовательно, существует неотрицательная матрица C,обратная к матрице 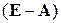 .
.
Третий критерий продуктивности. Матрица  продуктивна тогда и только тогда, когда сходится бесконечный ряд из матриц
продуктивна тогда и только тогда, когда сходится бесконечный ряд из матриц
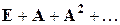 .
.
Можно доказать, что если этот ряд сходится, то его сумма равна 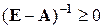 , иначе говоря, это один из способов вычисления искомой обратной матрицы. Если соотношение
, иначе говоря, это один из способов вычисления искомой обратной матрицы. Если соотношение
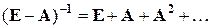
умножить справа на вектор конечного потребления y, то получим
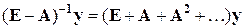 ,
,
или
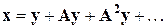 ,
,
что экономически можно интерпретировать следующим образом: чтобы обеспечить заданный объем конечного потребления y, необходимо не только произвести эти продукты, но еще и объем продукции 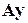 для обеспечения их выпуска. В свою очередь, для обеспечения выпуска
для обеспечения их выпуска. В свою очередь, для обеспечения выпуска 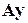 необходимо произвести
необходимо произвести 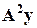 продуктов и т.д. Поэтому сумму
продуктов и т.д. Поэтому сумму 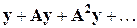 называют вектором полных затрат. Этот вектор совпадает с вектором валового выпуска x . Соответственно матрицу
называют вектором полных затрат. Этот вектор совпадает с вектором валового выпуска x . Соответственно матрицу 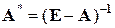 называют матрицей полных затрат. Для стоимостной модели каждый ее коэффициент
называют матрицей полных затрат. Для стоимостной модели каждый ее коэффициент  – это стоимость i-го продукта, затраченного при производстве единицы стоимости j-го продукта.
– это стоимость i-го продукта, затраченного при производстве единицы стоимости j-го продукта.
Предположим, что все коэффициенты матрицы 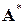 пропорционально увеличились, тогда для простого сохранения объема конечного потребления потребуется определенное увеличение валового выпуска. Однако при превышении некоторого порогового значения экономическая система вообще не сможет функционировать.
пропорционально увеличились, тогда для простого сохранения объема конечного потребления потребуется определенное увеличение валового выпуска. Однако при превышении некоторого порогового значения экономическая система вообще не сможет функционировать.
Запасом продуктивности матрицы A называют число 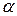 > 0, такое, что все матрицы
> 0, такое, что все матрицы 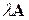 ,где
,где 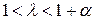 , продуктивны, но матрица
, продуктивны, но матрица 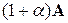 – не продуктивна.
– не продуктивна.
Условием продуктивности матрицы 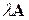 является существование неотрицательной матрицы
является существование неотрицательной матрицы 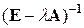 , что позволяет определить величину запаса продуктивности. Как правило, матрицы межотраслевого баланса обладают достаточным запасом продуктивности, например для СССР такой запас обычно был не менее 0,4.
, что позволяет определить величину запаса продуктивности. Как правило, матрицы межотраслевого баланса обладают достаточным запасом продуктивности, например для СССР такой запас обычно был не менее 0,4.